Um carro com tração dianteira percorre uma estrada que apresenta coeficiente de atrito igual a entre os pneus do carro e a própria estrada. Neste carro, tem-se uma distribuição de peso equivalente a do peso (carro + passageiros) nas rodas traseiras e do peso nas rodas dianteiras. Sabendo-se que , calcule a máxima aceleração que o carro pode atingir.
(a)
(b)
(c)
(d)
(e)
Passo 1
Vamos entender o que ele tá falando pra gente!
O motor de um carro tá ligado às rodas, certo? Já percebeu que é muito mais comum vermos carros com tração nas rodas dianteiras do que nas 4 ou só nas traseiras? Isso porque as rodas dianteiras estão mais próximas do motor. Então a força que o motor fornece às rodas dianteiras (tracionadas) é maior do que a traseiras, então a nossa aceleração máxima tá acontecendo nessa roda tracionada. Beleza até aqui?
Então, se a tração do motor faz a roda querer girar, nisso que ela gira, a roda empurra o chão pra trás e o chão, por reação, empurra a roda pra frente. Então se a gente fizer o diagrama de corpo livre para a roda, temos:
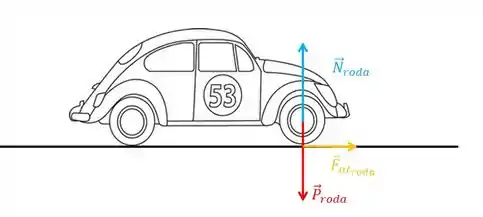
Passo 2
Então, pela segunda lei de Newton:
Na horizontal:
Na vertical:
Como, nesta roda só temos do peso:
Voltando para a equação da aceleração, que é o queremos:
Substituindo os valores:
Então:
Resposta
Alternativa (d)