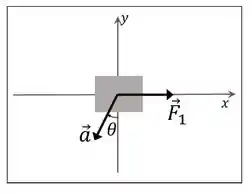
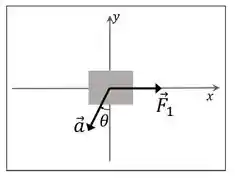
Duas forças () agem sobre uma caixa de massa que desliza livremente sobre uma superfície plana. Na figura, temos uma vista de cima da situação, mas apenas uma força é mostrada além do vetor aceleração da caixa. Considerando que o módulo da força , a aceleração da caixa tem módulo igual a e o ângulo , a única afirmação incorreta é:
(a) O módulo da componente horizontal da força é maior do que o módulo da componente horizontal da força .
(b) O módulo da força resultante é igual a .
(c) A componente vertical da força resultante possui o mesmo módulo que a componente vertical da força
(d) O módulo da força é maior que o módulo da força resultante
(e) O módulo da componente horizontal da força é menor do que o módulo da componente horizontal da força .
Passo 1
Na figura a gente só ta vendo a força e a . Mas tem a força , que não estamos vendo, mas ela tá lá.
Então, vamos usar a segunda lei de Newton.
Mas quem é a
É isso aqui:
Então:
Olhando pra figura do enunciado:
Temos que:
Decompondo o vetor aceleração, usando a regra do COlado e do SEparado, vemos que a componente em y é COs e a componente em x é SEn . Ambas são negativas porque apontam no sentido contrário ao que adotamos como positivo.
Show!
Voltando pra segunda lei de Newton:
Substituindo os valores que ele dá no enunciado:
Resolvendo isso:
Tá bonito!! Bora ler as alternativas.
Passo 2
(a) O módulo da componente horizontal da força é maior do que o módulo da componente horizontal da força .
Temos que
E
O módulo da componente horizontal de cada uma é:
Ou seja,
Beleza! Essa tá certa!!!
Passo 3
Vamos pra próxima.
(b) O módulo da força resultante é igual a .
A força resultante é:
Calculando o módulo, temos:
Resolvendo:
Então essa tá certa também!
Passo 4
(c) A componente vertical da força resultante possui o mesmo módulo que a componente vertical da força
Vimos que
E
A componente vertical é igual! Então essa tá certa!
Passo 5
(d) O módulo da força é maior que o módulo da força resultante
Vamos calcular o módulo de .
Resolvendo isso:
E já calculamos
Então essa tabém tá certa!
Passo 6
(e) O módulo da componente horizontal da força é menor do que o módulo da componente horizontal da força .
O módulo da componente horizontal da força é
O módulo da componente horizontal da força é
Então:
Opa!! Essa tá errada!!
Resposta
Alternativa E.