Um elétron com penetra horizontalmente em uma região onde está sujeito a uma força vertical constante de . A massa do elétron é . Determine a deflexão vertical sofrida pelo elétron enquanto percorre uma distância horizontal de
Passo 1
Vamos fazer um desenho para facilitar a compreensão:
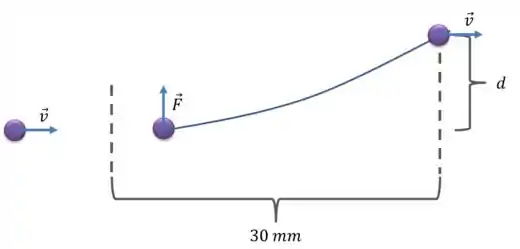
Bom, como a força atua na vertical sobre a partícula, a aceleração também será apenas na vertical.
Ou seja, temos um Movimento Uniformemente Variado em .
Além disso, como a velocidade na horizontal não varia (não há aceleração horizontal), a particula realiza um Movimento Uniforme em .
Passo 2
Agora que sabemos a direção e o sentido da aceleração do elétron, precisamos descobrir seu módulo. Temos a força aplicada a ele e a massa do mesmo. O que podemos usar? Isso mesmo! A segunda lei de Newton!
Substituindo os valores de e :
Passo 3
Como já vimos que a velocidade horizontal se mantém a mesma, para descobrirmos o tempo que o elétron demora para percorrer os , basta lembrar que este é um MRU:
Então, podemos utilizar a equação:
Passo 4
Conhecendo o quanto esse movimento durou, podemos analisar o movimento na vertical .
Como a partícula só apresenta velocidade na horizontal inicialmente, temos:
Então, temos:
Substituindo os valores encontrados: