USP; Sem campus; Álgebra Linear 2; P1; 2022; Questão 1
Sejam considere o subespaço
do espaço vetorial . Se , então é igual a:
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. descobrir o valor de , e para isso, é informado que , onde
E aí? alguma ideia de como começar? Talvez seja interessante representarmos os elementos de de outra forma.
Passo 2
Bem, vamos começar representando os elementos de em outra base, vamos fazer isso para as coisas ficarem mais simples. Vamos escolher uma base para . Alguma ideia? Podemos usar a base mais simples a
Dessa forma, cada vetor de pode ser representado como:
Passo 3
Agora que temos uma representação melhor para trabalharmos, vamos analisar a seguinte informação do enunciado:
Mas tem três vetores, logo para essa afirmação ser verdadeira é necessário que um vetor de seja combinação linear de outros vetores. Vamos montar a matriz contendo os vetores como linhas e escalonar ela para verificar a condição para os vetores serem LD. Montando a matriz, temos:
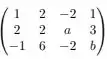
Vamos fazer as seguintes operações nas linhas
Com isso, temos:
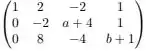
Por fim, fazemos
Obtemos assim a matriz
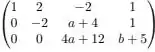
Passo 4
Qual a condição necessária para a ter dimensão se a matriz escalonada que obtemos é
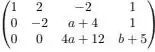
Ora, ela precisa ter uma linha inteira zerada, pois o processo de escalonamento é uma combinação linear das linhas da matriz e isso implicaria nelas sendo LD. Logo precisamos que
Logo, temos que
Valor presente na alternativa
Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊