1) Calcule as integrais abaixo usando uma substituição trigonométrica adequada.
(b)
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês? Bora lá resolver mais uma questão!!

O enunciado dessa questão já nos ajuda bastante! Ele afirma que temos que usar substituição trigonométrica. Então o que nos resta agora é determinar qual substituição trigonométrica vai se encaixar melhor na nossa situação aqui!
Meu deus, mas como fazemos isso mesmo?
Calma! Pra usarmos o método da substituição trigonométrica, é importante que a nossa função possua uma raiz com essa carinha aqui: .
Olha só que legal, a nossa raiz presente ali na integral tem essa carinha!
A gente pode ver ali que , então nosso será igual a !
Mas e agora o que eu faço com essa informação?
Vamos desenhar o nosso triângulo retângulo e fazer algumas interpretações!
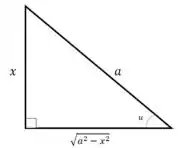
A partir disso, podemos fazer a seguinte relação trigonométrica:
Disso, podemos obter sua derivada :
Nós já temos o nosso valor de , mas para ficar mais fácil, ainda não vamos usar ele aqui! Assim a manipulação da nossa integral ficará bem mais fácil, e chegaremos ao mesmo resultado!
A partir das equações , podemos reescrever a nossa integral:
Bora lá trabalhar com isso então!
Passo 2
Vamos começar colocando em evidência no denominador:
Agora podemos cortar os dois presentes ali:
Vamos observar bem o nosso denominador agora. Você consegue ver a sacada que apareceu ali?
Temos uma identidade trigonométrica!!! Então,
Substituindo, vamos ter então:
Podemos simplificar essa expressãozinha, e também já substituirmos o valor de , já que nossa expressão está beeem mais simples!
Olha só que simples!
Agora vamos tirar aquele 2 da integral, já que ele é uma constante, e vamos trabalhar com essa nova integral no próximo passo!
Passo 3
Observando melhor a nossa integral ali do passo 2, vamos ter outra sacada! Temos mais uma identidade trigonométrica presente ali:
Tá, mas por que usar essa identidade? Para podermos trabalhar com a integral de senos e cossenos, eles não podem estar elevados ao quadrado. Então é sempre importante fazer relações de identidades trigonométricas que removam essa condição!
Vamos substituir então:
Como 1/2 é uma constante, vamos tirá-lo dali.
Agora, como temos uma subtração, podemos reorganizar nossa integral da seguinte maneira:
Bora lá então resolver cada uma dessas integrais separadamente!
Passo 4
Fazendo então a primeira integral, vamos ter que:
Porém, para a segunda integral, vamos observar que temos um ali multiplicando a nossa variável ! Mas por que isso é importante de ser notado?
É importante porque não existe uma resolução direta para a integral de senos e cossenos de valores como por exemplo.
Então, para podermos resolver isso, devemos adotar o método da integração por substituição em ! Aqui vamos chamar de já que a nossa integral está em função de .
Bora lá então!
Vamos adotar e .
Reescrevendo a integral vamos ter que:
Resolvendo essa integral e já substituindo de volta o valor de vamos ter que:
Porém, a partir das relações de identidade trigonométricas pode ser escrita por: ! Então:
Então, relembrando a nossa integral vamos ter que isso é igual a:
Passo 5
Voltando agora na nossa figura lá do passo 1, podemos assumir que:
Então, substituindo isso no nosso resultado encontrado ali no passo 4, temos que:
Como já definimos que , temos que:
Passo 6
Por fim, precisamos agora encontrar o nosso valor de . Mas como vamos fazer isso?
De novo vamos usar a nossa figura lá do passo 1!
Então, se , temos que !
Substituindo então vamos ter que:
Lembrando que esse é a nossa constante de integração!
Ufa!! Conseguimos!!!!

Pra essa questão é isso pessoal! Bora pra mais uma?