Calcule a integral
Passo 1
Até se a gente separar a integral em duas:
Parece difícil de resolver. O problema é esse denominador complicado. Então vamos dar uma mexida nele, assim:
Essa expressão lembra de leve essa identidade trigonométrica aqui:
E afinal, pra resolver uma integral vale tudo. Então, apesar de não ter nenhuma raiz, vamos apelar pra uma substituição trigonométrica:
Assim,
Passo 2
Daí a nossa integral vai ficar:
Como
Isso vai dar:
Passo 3
Vamos uma integral de cada vez, começando por essa aqui:
Ela sai tranquilamente com uma substituição simples
Daí:
Passo 4
Pra calcular a outra integral
Temos que lembrar da identidade trigonométrica
Então
Passo 5
Juntando tudo que achamos:
Ainda temos que voltar pra variável . Lembrando que:
A partir disso montamos o nosso triângulo retângulo da substituição trigonométrica:
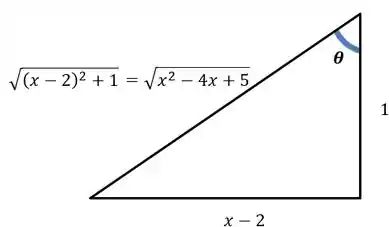
Passo 6
Pelo triângulo, podemos ver que
Daí temos que
Ah, e também:
Passo 7
Pronto! Agora podemos escrever o resultado em função de :