Calcule as seguintes integrais:
Passo 1
Essa é a cara de uma integral por substituição trigonométrica! Pelo caso da raiz (temos ali algo como , vamos colocar como tangente, assim:
Vamos levar isso para integral então:
Vamos trocar a tangente e a secante por senos e cossenos, fica assim:
Daqui basta fazer uma substituição e matar a integral:
Agora temos que voltar para . Para isso é só lançar a substituição inicial naquele triângulo auxiliar, como esse aqui, que nasce a partir de
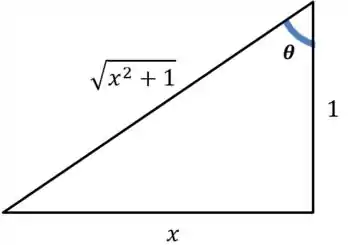
Nessa configuração, a cossecante é dada pela hipotenusa sobre o cateto oposto a , ou seja: