Calcule
onde é a fronteira da região definida por
orientada no sentido anti-horário.
Passo 1
Vamos fazer um esboço da curva:
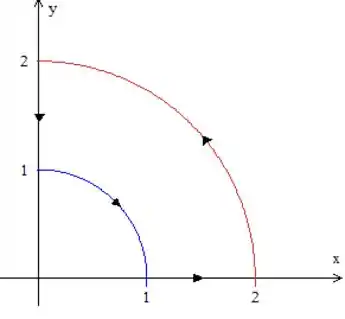
Como é o raio de uma circunferência, a região está limitada por uma circunferência de raio e outra de raio . Como temos e , tomamos apenas o 1º quadrante.
Essa curva (a fronteira da região) é formada por segmentos, cada um com uma parametrização. Isso ia gerar muito trabalho. Isso é uma dica de que pode ser uma boa usar o Teorema de Green, vamos tentar!
Passo 2
O campo vetorial da questão pode ser escrito como
Vamos agora calcular :
Passo 3
Agora podemos montar a integral. Aplicando o teorema de Green, a integral do enunciado pode ser escrita como:
Note que a curva está orientada positivamente!
Passo 4
Como a região está compreendida entre dois arcos de circunferência, a melhor saída aqui são as coordenadas polares. Faremos:
Pelo próprio gráfico, vemos que , o que equivale a de circunferência. Os valores de variam entre os dois arcos, logo . Temos, então:
Passo 5
Agora podemos calcular a integral. Integrando em relação a temos:
Passo 6
Integramos, então, em relação a :