Considere os seguintes sistemas lineares:
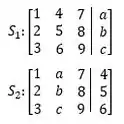
(I) Existem valores de a, b e c tais que o sistema não tem solução.
(II) Existem valores de a, b e c tais que o sistema não tem solução.
(a) I é verdadeira e II é falsa
(b) I é falsa e II é verdadeira
(c) Ambas são verdadeiras
(d) Ambas são falsas
Passo 1
Os dois sistemas e têm três equações e três incógnitas (que são os valores de x, y e z que satisfazem as três equações simultaneamente).
Precisamos ver se existem valores de a, b e c que façam com que esses sistemas tenham solução (ou seja, as três equações de cada um deles não podem ser incompatíveis).
Para isso temos que escalonar as matrizes aumentadas e analisar a existência de solução a partir daí.
Passo 2
Vamos começar com o sistema .
Escalonando a matriz aumentada:
(i) e
(ii)
Para que o sistema tenha solução, o termo que restou do lado direito da última tem que ser 0.
Caso contrário teríamos 0 diferente de 0 na última linha.
Então:
Para valores de a, b e c que não satisfazem essa relação, o sistema não tem solução.
Portanto, (I) é verdadeira: existem valores de a, b e c tais que o sistema não tem solução.
Passo 3
Agora vamos ver o sistema .
Escalonando a matriz aumentada:
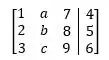
(i) e
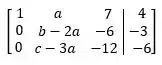
(ii)
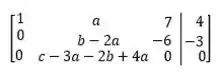
Notem agora que, para qualquer valor da variável y que multiplica o termo do meio, a equação será satisfeita, bastando que essa variável seja igual a 0.
Portanto, o sistema sempre tem solução, não existindo valores de a, b e c que façam com que ele seja impossível.
A afirmação (II) é falsa.
Resposta
(a) I é verdadeira e II é falsa