A integral indefinida
É igual a:
Passo 1
Oi, tudo bem?
O problema nos deu essa integral aqui
E pediu para encontrarmos o resultado! Xí, ferrou! Mas não, calma!
Temos uma razão entre dois polinômios, sendo que o polinômio do numerador tem grau maior do que o do denominador, então aqui vai minha dica pra você resolver quando for assim:
 DIVISÃO DE POLINÔMIOS!
DIVISÃO DE POLINÔMIOS!
A ideia é simplificar ao máximo essa fração, e fazendo a divisão desses polinômios, podemos escrever o polinômio do numerador como uma multiplicação do denominador (que será nosso divisor) pelo quociente e somar com o resto
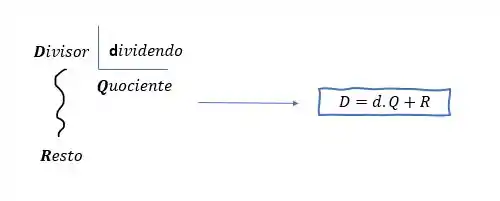
Assim vamos conseguir simplificar essa fração e poder integrar! Sempre que o numerador tiver potência maior que o denominador, quase sempre o caminho é esse!
Mas calma, vou fazer passo a passo com você!
Passo 2
O integrando dado foi esse aqui:
Vamos fazer a divisão do numerador pelo denominador :
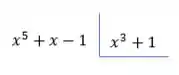
Pensa comigo, qual termo preciso multiplicar o para obter ? O ! Então é por aí que começamos o quociente!
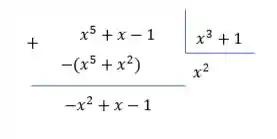
Como o grau do resto é menor do que o grau do divisor, paramos a divisão por aqui!
Tranquilo até aqui?

Agora vamos escrever o polinômio do denominador () como a multiplicação do quociente pelo divisor , mais o resto :
Aí temos
Beleza?
Passo 3
Agora vamos substituir essa fatoração no nosso integrando:

Separando em duas frações, já podemos cortar o termo e simplificar a primeira fração do lado direito!
Já na segunda fração precisamos de mais uns truques sujos! Aqui o truque é FATORAÇÃO DE CUBOS!
Esse truque vira e mexe aparece, e é sempre bom a gente relembrar:
No nosso caso e , então podemos escrever o denominador da segunda fração em termos dessa fatoração:

Viu ali o que apareceu? No numerador temos e no denominador que é o oposto do numerador! Então podemos simplificar e ficamos apenas com !
Ficamos com o seguinte:
Bem mais simples né?

Vamos integrar essa coisa agora?
Passo 4
Voltando para nossa integral:

A primeira integral vamos resolver pela regra da potência, e a segunda vamos fazer uma substituição simples e e ficaremos com a integral de que é :
E a resposta certa está na alternativa (B)!
E é isso! Espero ter ajudado!

Ufa! Terminamos!
Até próxima!