Dois blocos idênticos de massa ligados por um fio ideal estão dispostos como mostra na figura abaixo. O bloco , se encontra sobre uma superfície horizontal cujo coeficiente de atrito cinético vale enquanto o bloco encontra-se pendurado. O sistema parte do repouso e ambos os blocos tem a mesma velocidade até o momento em que o bloco toca a mola. A constante elástica da mola é desconhecida. Determine:
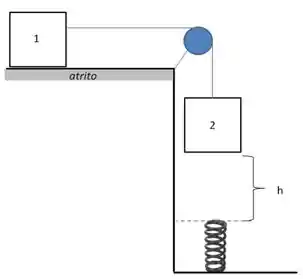
o trabalho realizado pela força de atrito no sistema quando o bloco cai uma altura . Este trabalho é positivo ou negativo? Justifique.
A velocidade do bloco ao tocar a mola.
Quando o bloco toca a mola, o fio entre os blocos é cortado instantaneamente. Observa-se que a velocidade do bloco neste instante é de . Sabendo que a compressão máxima que será produzida na mola é . Determine:
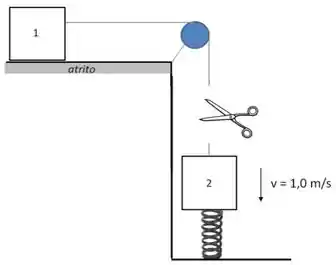
a constante elástica da mola em .
a que distância abaixo do ponto inicial de contato entre o bloco e a mola encontra-se o ponto de equilíbrio do sistema bloco e mola.
Passo 1
Para determinar o trabalho realizado pela força de atrito, devemos lembrar da definição de trabalho:
Pelo fato de existir um vínculo entre os blocos, se o bloco , cai uma altura de , isso significa que o bloco também se deslocou . Voltando à equação do trabalho, lembrando que a força de atrito cinético, nesse caso, é dada por , temos:
Substituindo os valores conhecidos, temos:
Pelo fato de a força de atrito se opor ao movimento, temos que o trabalho realizado é negativo, portanto:
Passo 2
Para determinar a velocidade do bloco ao tocar na mola, devemos utilizar o seguinte teorema que relaciona o trabalho das forças não conservativas com a variação da energia mecânica, pois existe uma força de atrito, que não é conservativa, atuando.
Já calculamos o trabalho realizado por essa força, ele vale . A variação da energia mecânica, pode ser determinada da seguinte forma:
Pensando em nosso sistema, que é composto pelos dois blocos, temos a seguinte variação da energia mecânica:
Lembrando que somente o bloco está variando de altura, ou seja, somente ele possui , além do fato de que por estarem ligados por um fio, os blocos possuem a mesma velocidade. Por partirem do repouso, a velocidade inicial é zero!
Substituindo os valores conhecidos, temos:
Passo 3
Para determinar a constante elástica da mola, vamos utilizar a conservação da energia mecânica, entre o momento antes de o bloco tocar na mola, e o momento em que a deformação é máxima:
Perceba que o meu potencial zero está na altura da deformação máxima da mola, que é . Substituindo os valores, temos:
Passo 4
Na situação de equilíbrio do sistema bloco mola, temos que satisfazer a seguinte relação:
Onde o peso do bloco deve ser igual à força elástica, temos então:
Substituindo os valores, temos:
Resposta
, negativo, pois a força de atrito se opõem ao movimento.