Um objeto de 20,0 g de massa é posicionado contra a extremidade livre de uma mola de constante elástica igual a 25,0 N/m que é comprimida de 10,0 cm. Uma vez liberado, o objeto desliza 1,20 m, sobre a mesa, e cai no chão a 1,40 m da borda da mesa, como esquematizado na figura. A distância de deslizamento na mesa inclui os 10,0 cm de compressão da mola e a superfície da mesa está a 1,20 m acima do nível do solo. (Use g = 10,0 m/.)
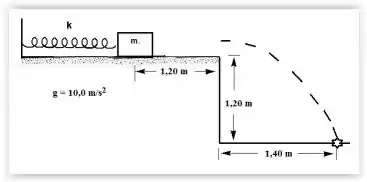
(a) Calcule a rapidez do objeto no instante em que perde contato com a borda da mesa.
(b) Mostre que existe atrito entre o objeto e a superfície da mesa.
(c) Calcule o coeficiente de atrito cinético.
Passo 1
O item (a) pede a velocidade do objeto no instante em que ele perde contato com a borda da mesa. Vamos analisar:
Percebemos que a trajetória de queda do objeto se trata de um lançamento horizontal.
No lançamento horizontal, o objeto inicialmente só velocidade no eixo, que se mantem constante durante todo o trajeto.
A velocidade no eixo y, inicialmente nula, varia de acordo com a ação da aceleração da gravidade.
Vamos definir como a velocidade do objeto ao alcançar a borda da mesa.
Assim, podemos montar as seguintes equações para descrevem o movimento do objeto desde o instante (t=0) em que abandona a mesa até atingir o solo:
(o eixo x está sobre o solo; o eixo y tem origem no solo e está orientado para cima):
Para que trata de um movimento retilíneo uniforme:
Definindo x como a distância percorrida pelo objeto em x, montamos:
Para que se trata de um movimento uniformemente variado, montamos:
Podemos descobrir o valor do tempo de queda, pois sabemos que no momento da queda y=0, ou seja, o objeto encontra o chão.
Temos o valor de h e de g:
h=1,20
g=10
Substituindo:
Show!
Agora podemos voltar para a equação do MRU do :
Sabemos que a distância percorrida em x foi 1,40 m.
Substituindo:
Passo 2
Agora vamos analisar o item (b).
Vamos mostrar que existe atrito entre o objeto e a superfície da mesa.
Para verificar isso, podemos comparar energia mecânica do objeto quando é liberado com sua energia mecânica na borda da mesa.
Se tomarmos o nível zero da energia potencial gravitacional na superfície da mesa, teremos inicialmente apenas energia potencial elástica da mola e, no fim, apenas energia cinética:
Assim:
Podemos perceber que a energia mecânica final é menor do que a energia mecânica inicial. Isso se dá pela existência do atrito que dissipa essa energia mecânica.
Passo 3
Agora vamos calcular o valor do coeficiente de atrito cinético.
Sabemos que como não há força externa aplicada ao sistema mola-objeto-mesa-Terra, toda energia mecânica dissipada da posição inicial do objeto até a borda da mesa foi causada pelo atrito.
Podemos relacionar o trabalho do atrito com a variação de energia mecânica da seguinte forma:
Sabemos do passo anterior que
Sabemos também que
E que
Agora, podemos aplicar:
Sendo d, a distância que o objeto percorreu de sua posição inicial até a borda da mesa:
Assim,