Na figura abaixo estão indicadas 3 posições identificadas pelas letras , e . Um Bloco de massa inicialmente em repouso a uma altura a partir do solo está em contato com uma mola comprimida. A mola possui constante elástica .
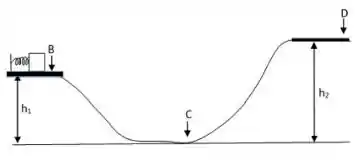
Após a mola ser solta e o bloco se desprender, o bloco desliza sem atrito passando pelo ponto que se encontra na mesma altura . Segue descendo por uma rampa até o ponto . Neste ponto o bloco possui velocidade . Após passar o ponto , o bloco volta a subir por uma segunda rampa de altura até uma plataforma horizontal. Esta plataforma possui atrito e o bloco desliza até parar no ponto . O coeficiente de atrito cinético na plataforma vale .
Use para a aceleração da gravidade. As variáveis dadas do problema são (, , , , e )
a) Determine a compressão da mola em termos das variáveis dadas do problema.
b) Determine a velocidade do bloco no ponto em termos das variáveis do problema.
c) Determine a distância percorrida na plataforma em termos das variáveis dadas.
d) Calcule a menor altura de modo que acima dela o bloco volta a tocar na mola.
Passo 1
Ao longo desse problema, um ponto é vital de ser analisado.
A Energia Mecânica se conserva ou não?
A resposta é sim, a energia mecânica se conserva.
Isso acontece pois a Força Peso e a Força Elástica atuando sobre o bloco são forças conservativas, ou seja, não retiram energia do sistema. Já a Força Normal não é uma força conservativa, porém, ao longo de todo o trajeto ela atua perpendicularmente ao deslocamento, não realizando trabalho, ou seja, não alterando também a energia do sistema.
Feita essa análise, podemos utilizar a conservação da energia mecânica para resolver cada um dos itens.
Passo 2
Na letra (a), queremos achar a compressão da mola .
Para isso, precisamos percorrer o caminho inverso do bloco.
Temos informação sobre a velocidade no ponto e além disso, sabemos a variação de altura entre o instante inicial e o ponto , então conseguimos comparar as energias cinéticas e potenciais entre esses instantes.
Como a energia mecânica se conserva, podemos dizer que a energia mecânica inicial é igual a no ponto :
No instante inicial (mola comprimida), o bloco se encontra em repouso, portanto sua energia cinética é nula.
Porém, ele tem uma energia potencial elástica associada à deformação da mola e uma energia potencial gravitacional associada à sua altura a partir do solo.
Então sua energia mecânica será:
Já no ponto , não há nenhuma energia potencial elástica nem gravitacional, toda a sua energia mecânica está na forma de cinética:
Passo 3
Utilizando a equação da conservação da energia, temos:
Queremos a compressão da mola, então vamos isolar esse termo:
Achamos a compressão da mola no instante inicial.
Passo 4
Na letra (b), queremos a velocidade no ponto .
Ainda partindo da conservação da energia mecânica, podemos novamente comparar as energias do ponto e do ponto :
Por que estamos utilizando tanto o ponto ?
Porque sabemos que a energia potencial elástica e gravitacional nesse ponto são nulas e além disso conhecemos a velocidade nesse ponto e portanto sua energia cinética, ou seja, temos todas as informações.
Já vimos no Passo 2, que:
Já no ponto , não há mais energia potencial elástica (não há deformação de nenhuma mola). A energia mecânica nesse ponto está na forma de potencial gravitacional associada à altura e também na forma de energia cinética associada à velocidade :
Aplicando na conservação da energia, temos:
Vamos isolar . Podemos cortar as massas :
Achamos a velocidade no ponto .
Passo 5
Na letra (c), queremos saber a distância percorrida na região com atrito.
Quando o bloco entrar na região com atrito, essa força vai dissipando a energia cinética do bloco até que ele pare no ponto .
Então, para achar essa distância , precisamos primeiro saber qual a energia cinética com que o bloco está chegando na plataforma horizontal para calcular ao longo de qual distância que ela será dissipada.
Para isso, vamos conservar a energia mecânica entre o ponto e um novo ponto que chamaremos de (antes do trecho com atrito):
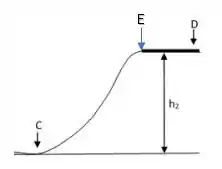
No ponto , já vimos que a energia está apenas na forma de cinética:
Já no ponto , teremos tanto uma energia cinética, quanto uma energia potencial gravitacional associada à altura :
Aplicando na conservação de energia, temos:
Ou seja, agora, sabemos qual a energia cinética com que o bloco está entrando na região com atrito.
Passo 6
Agora, vamos utilizar o Teorema Trabalho-Energia Cinética:
Onde o trabalho resultante é a variação da energia cinética.
Como a força de atrito é a única realizando trabalho nesse trecho, temos:
A energia cinética final será nula, já que o bloco estará parado, enquanto a energia cinética inicial é .
Ou seja, a ideia é que quando a força de atrito retirar do bloco a quantidade de energia que ele tem de cinética, ele vai parar.
Passo 7
Vamos calcular o trabalho da força de atrito .
O trabalho será o produto escalar entre o vetor e o vetor delocamento :
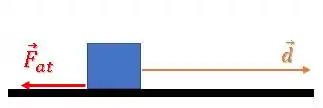
Esse produto escalar pode ser calculado com o produto dos módulos vezes o cosseno do ângulo entre eles:
Como os vetores estão na mesma direção e sentidos opostos, o ângulo entre eles é:
Então:
Beleza, e quem é essa força de atrito ?
Passo 8
A força de atrito cinético é dada por:
Onde é o coeficiente de atrito cinético e a força normal da superfície.
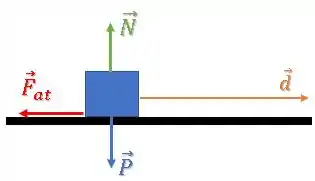
Como o corpo está em equilíbrio na vertical, temos que:
Então, a força de atrito é:
E o trabalho dessa força:
Passo 9
Voltando ao teorema, ficamos com:
Cortando e isolando , ficamos com:
Essa será a distância percorrida no trecho com atrito até o bloco parar.
Passo 10
Na letra (d), queremos a menor altura para que o bloco volte até a mola.
Como assim para que o bloco volte a tocar a mola?
Dependendo do valor da altura , o bloco não terá energia suficiente para subir a rampa, ficando parado no final dela (ponto ):
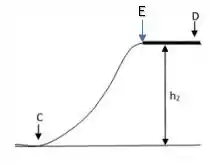
Então, a ideia é considerar que a energia cinética no ponto é nula e toda sua energia mecânica está na forma de energia potencial gravitacional:
Podemos calcular a conservação a partir do ponto , pois já sabemos que toda sua energia nesse ponto está na forma de cinética:
Fazendo a conservação, temos:
Resposta
(a)
(b)
(c)
(d)