Um grande bloco de massa deve ser transportado horizontalmente através de uma distância total de sobre um piso com atrito. Um trator empurra o bloco durante os primeiros com uma força variável, descrita pelo gráfico abaixo.
Tome .
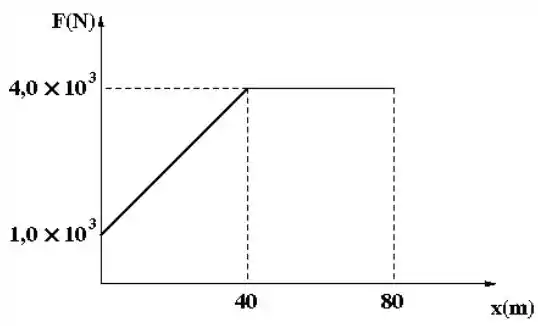
a) Calcule o trabalho total realizado pelo trator sobre o bloco.
b) Sabendo que o bloco chega totalmente em repouso ao fim dos , encontre o coeficiente de atrito cinético entre o bloco e o piso.
c) Ache a velocidade do bloco na posição .
Passo 1
a)
Basta calcular a área do gráfico! :)
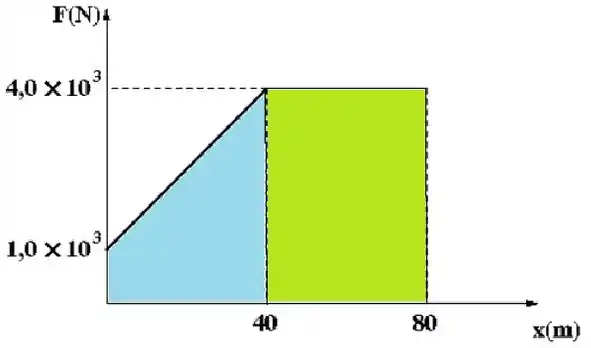
A área do trapézio azul é:
Show! E pra área do retângulo verde, temos
Então a área total do gráfico é:
Então o trabalho do trator sobre o bloco é .
Passo 2
b)
Pelo teorema trabalho-energia cinética, temos:
Repare que o bloco começa o trajeto do repouso e também termina em repouso. Logo,
Ou seja:
Passo 3
Além disso, nessa questão só temos o trabalho do trator e o do atrito, então
E o trabalho do trator já calculamos na letra (a)!
Logo,
Passo 4
Por outro lado, temos
- é a força de atrito:
- é a distância na qual o atrito atua, ou seja a distância percorrida pelo bloco:
- é o ângulo entre o sentido da força de atrito e o deslocamento do bloco. Como o atrito se opõe ao movimento:
Portanto, temos
O enunciado nos dá e então:
Passo 5
Beleza, pelo teorema trabalho-energia cinética, achamos
E calculando o trabalho, obtivemos
Portanto:
Passo 6
c)
Agora queremos a velocidade do bloco com .
Podemos usar de novo o teorema trabalho-energia cinética!
Note que a partir dos , o trator não empurra mais o bloco, logo
Ou seja, de a , temos
Já vimos que o bloco está em repouso com , então . Portanto,
E como :
Passo 7
Beleza, então vamos calcular o trabalho realizado pela força de atrito entre e :
Usando , e , isso dá:
Passo 8
Ótimo, estamos quase acabando! Vimos que
E acabamos de achar , então a equação vai ficar
Resposta
a)
b)
c)