Duas caixas de massas e deslizam para baixo em um plano inclinado com com a horizontal. As caixas são ligadas por uma haste rígida sem massa paralela ao plano, conforme a figura ao lado. O coeficiente de atrito cinético entre a caixa e o plano é ; e entre a caixa e o plano é .
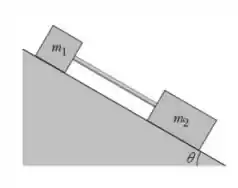
Qual a tração na haste?
Qual a aceleração das massas?
Se as posições das caixas fossem invertidas, o que mudaria nas respostas anteriores? Explique fisicamente a diferença.
Passo 1
Eaew, tudo certo contigo?
Aqui temos um problema de plano inclinado, mas o nosso bloquinho é um pouco mais complicado que o normal! Os blocos têm massa e , deslizam cada um com um coeficiente de atrito diferente com a superfície, respectivamente, temos e . Dada que a inclinação do plano é de precisamos encontrar
Alternativa , a tração na haste, em que vamos precisar montar o diagrama de forças e utilizar a segunda lei de Newton para relacionar as forças presentes no sistema!
Alternativa , a aceleração das massas, lembrando que este corpo se move como um só, já que a haste é rígida, a expressão para a aceleração vai ser obtida manipulando as equações que obtivemos na alternativa anterior
Alternativa Será que mudar a posição das caixas faz alguma diferença? Pense um pouco sobre isso, mas é uma questão conceitual! No final discutimos com mais calma!
Vamos resolver então este problema! Bora lá!
Passo 2
Antes de tudo, vamos fazer o diagrama de forças, temos o seguinte
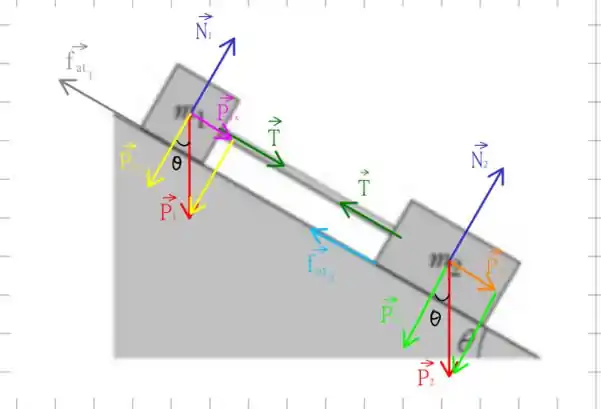
A segunda lei de Newton diz que
para cada um dos corpos, em cada direção independente do sistema. Nós temos duas direções que importam, a paralela ao plano e a perpendicular ao plano. Primeiro, para o corpo de massa , temos a equação paralela ao plano como
e, a equação perpendicular ao plano, temos que
igual ao vetor nulo, pois não há movimento perpendicular ao plano! De maneira bastante análoga temos para o corpo de massa , as seguintes equações
e, também que
Todas essas equações estão escritas em suas formas vetoriais. No próximo passo vou escrevê-las sob a escolha de que o sentido positivo é para baixo, assim como lembrar de algumas definições! Belezinha? Saca só!
Passo 3
Considerando como a direção paralela ao plano como e com sentido positivo descendo pelo plano, e para a direção perpendicular com sentido positivo apontando para fora do plano, temos que nossas equações se tornam
Vamos usar estas quatro equações para obter a tração . Primeiro, vamos obter quem são as componentes de ambas as forças peso, e as forças de atrito, em termos dos dados do enunciado! Vem comigo!
Passo 4
Para ambas as forças peso podemos montar o seguinte triângulo retângulo
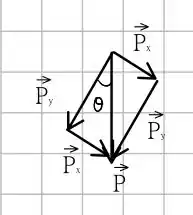
Portanto, para cada uma delas podemos identificar que
e, também que
Agora, vamos obter as forças de atrito! Lembra qual é a definição? Saca só!
Passo 5
A força de atrito cinético é definida como
se o sentido positivo de é o sentido do movimento (em nosso caso SIM!). Usando as equações e temos que a força normal pode ser obtida em termos de para cada bloquinho, temos que
e, portanto, a nossa força de atrito pode ser escrita como
Vamos agora voltar para as equações que dominam o movimento! E reescrevê-las! Vamo que vamo!
Passo 6
As equações que importam agora são apenas as equações e , temos que elas podem ser escritas como
Vamos dividir por e por apenas para simplificar, temos que
Note que como as acelerações são iguais para os dois bloquinhos (eles se movem juntos), podemos simplesmente igualar as duas equações acima e obter
podemos cortar os termos de e colocar ambas as trações do mesmo lado da equação, obtendo
Colocando termos comuns em evidência, podemos obter a seguinte expressão
Fazendo um MMC podemos escrever que
De forma, que podemos isolar a nossa tração como
Maravilha! Agora é só substituir valores! E obtemos que
Maravilha! A primeira alternativa já foi! Vamos fazer a próxima agora! Bora lá!
Passo 7
Precisamos achar a aceleração agora! Eu guardei a equação para isso, pois substituindo ela na equação ou , obtemos que
dividindo tudo por , evidenciando , temos que
Portanto, temos que a aceleração será dada por
Substituindo valores, temos que
Aí está a nossa aceleração! Vou rapidamente discutir a alternativa aqui, note pelo conjunto de equações de à , que alterar a ordem das caixas seria indiferente, já que o corpo se move como um só! Então, não faria diferença alguma! A questão é isso pessoal! Te vejo na próxima! Tchau Tchau!
Resposta
, e inverter as caixas não muda o resultado!