Energia Potencial e Conservação da Energia Mecânica
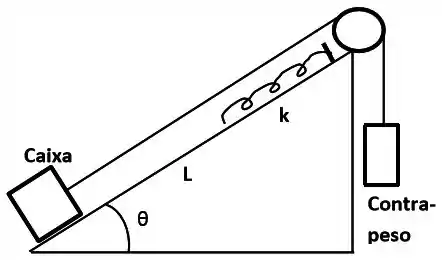
O deslocamento de uma carga da base de um plano inclinado até o topo é feito por um dispositivo análogo ao da figura ao lado. Ele é constituído por uma caixa, de massa , presa na extremidade de um cabo. O cabo passa por uma roldana no topo do plano inclinado e tem um contrapeso, de massa , em sua outra extremidade. Próximo ao topo existe uma mola de constante elástica . As superfícies da caixa e do plano inclinado são rugosas, com coeficiente de atrito cinético . O ângulo que o plano inclinado faz com a horizontal é 25°. Liberando o contrapeso a partir do repouso, a caixa é puxada pelo cabo. Ela pode transportar cargas de até , por uma distância , desde a base do plano até o ponto de máxima compressão da mola , quando então a caixa é parada pela mola, antes que o contrapeso chegue ao solo. Considere o cabo e a roldana ideais. Utilize ; e .
a) Use conceitos de trabalho e energia para obter a compressão máxima da mola em função de , , , , , , , e quando a caixa estiver com a carga máxima. Calcule o valor de .
b) Encontre a expressão teórica para a velocidade máxima da caixa. Utilize para a compressão máxima da mola e despreze o atrito neste caso. Responda em função das variáveis do problema.
Passo 1
(a)
Considerando a caixa com carga máxima, podemos utilizar o teorema trabalho-energia, temos então:
A força normal é sempre perpendicular a trajetória, então ela não realizará trabalho. Fica assim:
Passo 2
(b)
A velocidade máxima da caixa ocorre quando a aceleração nela for zero, ou seja, o somatório das forças será nulo:
Portanto, a distância percorrida pela caixa é . A equação de conservação da energia mecânica toma a forma:
Resposta
(a)
(b)