Um bloco de massa inicialmente em repouso desliza para baixo em um plano inclinado que faz um ângulo com a horizontal. Depois de ter deslizado uma distância , o bloco colide com uma mola de constante elástica desconhecida. A mola reduz a velocidade do bloco até fazê-lo parar momentaneamente. Neste instante a mola está comprimida de uma distância . Não existe atrito entre o plano e o bloco até o contato com a mola (deslocamento ). Mas existe atrito entre plano e o bloco na região da mola (deslocamento ) com coeficiente de atrito cinético . Use para a aceleração da gravidade. Responda em função dos dados fornecidos utilizando a Lei de Conservação de Energia.

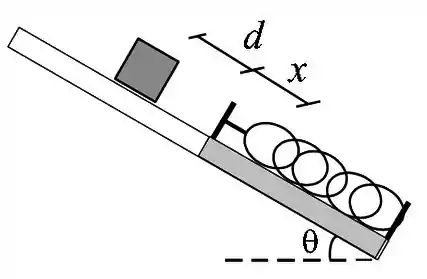
(b) Determine a energia potencial elástica armazenada na mola após ela ter sido totalmente comprimida, em função das variáveis dadas.

Cortar a(s) parcela(s) que não temos

Bem, nem todas as parcelas vão estar presentes! Então fique atento porque do repouso até a compressão máxima da mola, a velocidade do bloco não muda e é exatamente 0. A parcela de variação da energia cinética a gente vai cortar, beleza?

Calcular a energia potencial gravitacional

Já que não cortamos a parcela da energia potencial gravitacional, temos que dar nosso jeito para encontrar uma expressão com informações que conhecemos. Então, tá valendo a seguinte fórmula:

Opa, mas quem é esse que surgiu do nada? Conhecemos a massa e a aceleração da gravidade mas o por enquanto é desconhecido. Ta na hora de conhecer então! Dá uma olhada nesse esquema:

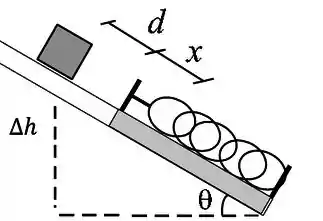
Agora, por trigonometria, a gente consegue descobrir o quanto o bloco caiu não é? Vamos ter então:

A gente usa um sinal de negativo porque a altura final é mais baixa que a altura inicial no nosso referencial, tá? É importante lembrar que “” é sempre uma variação entre final e inicial. Agora, tudo que falta substituir na fórmula e chegamos a simpática expressão:

Calcular o trabalho das forças não conservativas

Antes de mais nada, é importante identificar quais são as forças não conservativas atuando. Então, vamos ter:

Como a força de atrito atua no sentido contrário do deslocamento, o trabalho da força de atrito vai ser então negativo, beleza? Mas e o módulo de ? Como descrever ele? Dá uma olhada nessa expressão:

Onde “” é a força normal sobre o bloco, perpendicular à rampa. Como o nosso bloco não saiu magicamente da rampa, podemos igualar a normal à uma componente do vetor peso.

O diagrama do corpo livre do bloco não nos deixa dúvida de qual componente igualar:

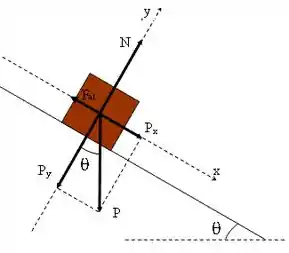
Pelo diagrama, a gente vê que:

Agora que sabemos tudo, basta substituir! Vamos lá:

Unir os resultados anteriores

Antes, tínhamos somente essa fórmula:

E não sabíamos nada sobre ela. Mas agora, podemos expressar a energia potencial elástica em termos de números conhecidos! Pra isso, só substituir galera:

Considerando que o “” de inicial é a situação da mola relaxada e “” da mola comprimida ao máximo, não vamos ter energia potencial elástica inicial, certo? Lembre que ela é uma função da deformação então não pode existir se a deformação é nula.