Um bloco de massa e dimensões desprezíveis encontra-se sobre um plano horizontal. Ele comprime uma mola de constante elástica no pondo de uma distância em relação à posição ; conforme mostra a figura. Liberado neste ponto a partir do repouso ele percorre o trajeto perdendo contato com a mola no ponto , onde a mola está relaxada. Somente entre e , separados de uma distância desconhecida há atrito. O coeficiente de atrito cinético entre as superfícies do bloco e do plano na região . Após o ponto há uma rampa sem atrito. A partir do ponto , final da rampa, a superfície é horizontal e tem uma altura em relação à horizontal do trecho ; vide a figura.
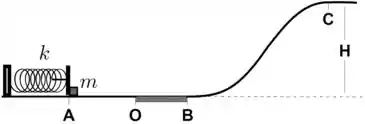
- Determine a velocidade do bloco no ponto ;
- Determine a distância entre os pontos e , dispondo que a velocidade do bloco em é nula;
- Determine a compressão mínima, , da mola necessária para que o bloco atinja o ponto no topo da rampa.
Passo 1
Vamos primeiro escrever os dados do enunciado
Isso vai servir para conferirmos se nossas respostas estão de acordo com os dados que temos.
Passo 2
Vamos considerar o chão como sendo o local onde o bloco começa o movimento.
a)
Não temos atrito nem outras forças dissipativas ao longo de . Então
Vamos achar a energia mecânica em cada ponto, começando pelo ponto .
Porque não temos velocidade, e o bloco está no chão. Então
Como a mola vai estar relaxada em , a deformação dela em é a distancia de para .
Então
Passo 3
Vamos agora achar a energia mecânica no ponto .
Porque a mola está relaxada, e o bloco está no chão. Então
Passo 4
Então temos
Passo 5
b)
Nesse trecho temos a força de atrito atuando, que é uma força dissipativa então teremos
Já temos a energia mecânica em . Precisamos encontrar a energia mecânica em e o trabalho da , vamos chamar de a distancia entre e .
Já vimos em muitos outros exercícios que, no caso do bloco no plano
Então
Passo 6
Temos que encontrar a energia mecânica em
Ela é zero, porque não temos energia potencial gravitacional, por estarmos no chão, não temos energia potencial elástica por não ter mola em contato, e não temos energia cinética porque a velcodaide é zero.
Passo 7
Juntando todas essas formulas
Podemos substituir a energia mecânica em pela energia potencial elástica, por que até esse ponto não há perda de energia (lembra do Passo 4?):
Passo 8
c)
A compressão mínima deve ser tal que a energia cinética no ponto seja zero, que é a menor quantidade de energia necessaria.
Como temos o trecho que gera uma perda de energia devemos ter
Já vimos no item b) que
E também vimos no item a) que dado a compressão da mola
Passo 9
Falta descobrirmos a energia mecânica em .
Isso acontece porque a velocidade é zero, e não temos mola enconstando no bloco nesse ponto.
Passo 10
Recaptulando temos
Então