Água escoa suavemente pela tubulação cilíndrica da figura ao lado, preenchendo-a completamente. As secções 2 e 3 têm o mesmo diâmetro.
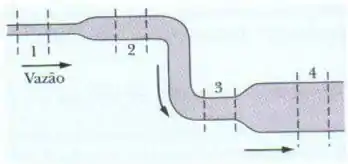
Na mesma tubulação, como se relacionam as pressões em cada região?
Passo 1
Precisamos usar aqui a equação de Bernoulli:
Passo 2
Vamos olhar primeiro entre 1 e 2, que estão na mesma altura, então . Cortando o da equação:
Pelo princípio da continuidade, . Como a , então .
O segundo termo vai ser negativo, então, .
Passo 3
O 2 e 3 têm o mesmo diâmetro, então pelo princípio da continuidade , . Podemos cortar a velocidade da equação:
Como a profundidade de 3 é maior do que a de 2, , o segundo termo vai ser positivo, o que vai fazer com que .
Passo 4
Finalmente, entre 3 e 4, as profundidades são iguais, então, cortanto esse termo temos:
Pelo princípio da continuidade, como , então . Assim, o segundo termo da equação acima será negativo, o que faz com que .
Juntando tudo, chegamos em:
Resposta
E)