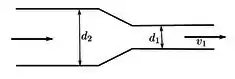
Um fluido incompressível com densidade escoa por uma tubulação horizontal e sai para o ar livre (a pressão atmosférica patm), com velocidade v1, após passar por um estrangulamento, no qual o diâmetro da tubulação diminui de d2 para d1. A pressão manométrica p2 - patm na tubulação, antes do estrangulamento, é dada por:
a)
b)
c)
d)
e)
f)
Passo 1
Nessa questão a gente vai ter que usar Bernoulli e o Princípio da Continuidade. Esse último diz pra gente que:
As respostas estão em função de , então não precisamos nos preocupar com ele. Isolando nessa equação aí de cima:
As áreas a gente calcula:
E substituindo em :
Passo 2
Show! Agora vamos usar Bernoulli:
As alturas e são iguais, então podemos cortar! A pressão vai ser a pressão atmosférica , então:
Substituindo o valor que achamos pra :
Que é a pressão manométrica.
Resposta
Letra F.