Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Considere um sistema formado por um reservatório de água com área e altura . O reservatório está conectado na parte inferior com uma tubulação cuja seção transversal tem área . A uma distância da base do reservatório, a tubulação faz uma curva de 90 graus mantendo a seção transversal com a mesma área e ficando paralela ao solo. Em seguida, a tubulação se conecta com uma outra de área , cuja extremidade está aberta permitindo que a água saia com velocidade para o meio externo. Considere que a velocidade com que a superfície do líquido no reservatório desce seja muito menor do que as outras envolvidas no processo. Suponha conhecidas a densidade da água , a aceleração da gravidade e a pressão atmosférica .
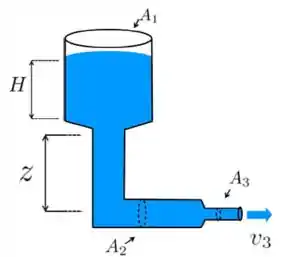
- Determine a velocidade no trecho horizontal de área em termos de
- Determine a pressão no trecho horizontal da canalização de área
Passo 1
a)
Podemos fazer a seguinte coisa: Aplicar Bernoulli entre a superfície do tanque e a saída da água, na canalização de área .
Por que não vamos aplicar direto na parte da canalização de área Porque não sabemos a pressão ali, então temos que encontrar a velocidade ali de forma indireta.
Já na parte , podemos tomar o extremo da saída de água, que está sujeito à pressão atmosférica. Além disso, podemos considerar o referencial da altura o próprio nível
Assim:
Considerando , já que desprezamos aa velocidade do fluido na superfície do reservatório, e sabendo que , além de (referencial) ficamos com:
Beleza?
Bom, com essa velocidade, basta a gente aplicar o princípio da continuidade entre os trechos :
Passo 2
b)
Pra achar a pressão no trecho , vamos aplicar novamente a equação de Bernoulli. Podemos aplicar entre o trecho 3 e o 2, por exemplo, já que eles estão na mesma altura, o que simplifica a expressão:
A pressão em é igual a atmosférica, e as velocidades foram encontradas nos itens anteriores:
Pronto (:
Resposta
a)
b)