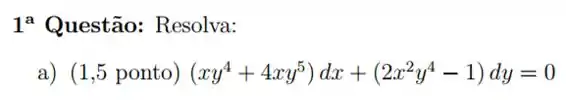
Passo 1
Essa equação tem cara de exata, né? Vamos ver se é mesmo:
e
Pelas derivadas parciais temos:
Assim a equação não é exata, vamos ver agora se existe um fator integrante para torna-la exata.
Passo 2
Vemos que:
Depende somente de isso é bom, então vamos calcular o fator integrante:
Assim, multiplicando a equação pelo fator integrante temos:
e
Agora sim temos uma equação exata e vamos resolver do jeito que já conhecemos.
Passo 3
Seja a solução da equação exata, então podemos escrever:
Vamos integrar a primeira equação em relação a , ok?
Derivando em relação a :
Então temos que a solução da equação é:
Resposta
Exercícios de Livros Relacionados
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores
Em cada um dos problemas de 1 e 12:(a) Desenhe um campo de direções para a equação diferencial dada.(b) Com base em uma análise do campo de direções, descreva o comportamento das soluções para valores