Resolva as seguintes inequações
Passo 1
Precisamos começar vendo como será aquele módulo
Vamos ver o sinal de
isso é uma função de segundo grau.
Vamos começar achando suas raízes
AS raízes vão ser
E
Como , o seu gráfico será algo assim
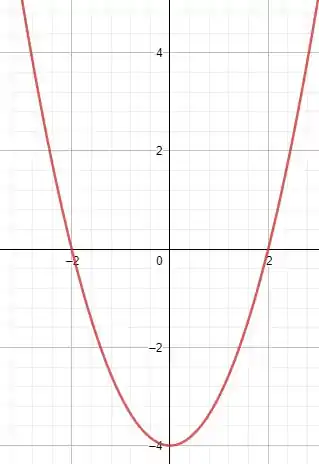
Entre as raízes é negativo e fora é positivo.
Assim, o módulo vai ficar
Passo 2
A inequação vai ficar
Precisamos analisar cada inequação dessa separadamente.
Passo 3
Vamos começar com
Onde
isso é uma função de segundo grau.
Vamos começar achando suas raízes
AS raízes vão ser
E
Como , o seu gráfico será algo assim
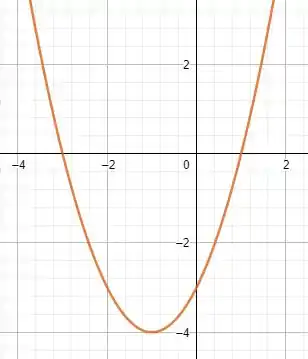
Entre as raízes é negativo e fora é positivo.
Como queremos a parte positiva o intervalo vai ser
Mas aqui, estamos no intervalo
Isso vai fazer com que só tenhamos
Passo 4
Vamos para
Onde
isso é uma função de segundo grau.
Vamos começar achando suas raízes
AS raízes vão ser
E
Como , o seu gráfico será algo assim
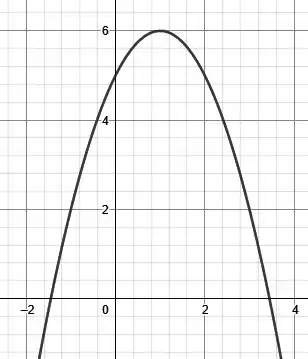
Entre as raízes é positivo e fora é negativo.
Como queremos a parte positiva o intervalo vai ser
Mas aqui, estamos no intervalo
E
Isso vai fazer com que só tenhamos
Passo 5
Agora vamos juntar as duas soluções
Isso vai nos dar