Resolva as seguintes inequações
Passo 1
Precisamos fazer os dos módulos e ver como será a expressão, primeiro vamos pegar
Resolvendo aquela inequação, vamos ter
E
Resultando em
E vamos ter
Passo 2
Vamos para o segundo módulo
Resolvendo aquela inequação, vamos ter
E
Resultando em
Passo 3
Vamos agora juntar todos esses módulos
Temos que olhar os intervalos primeiro, para entendermos como vai ficar
Então, no fundo temos
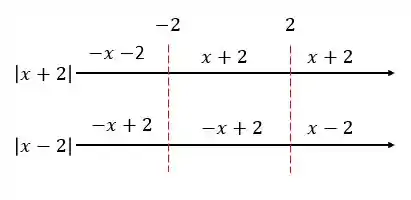
Fazendo a soma, vamos ter
Vai ficar
Vamos ter inequações para resolver em cada intervalo.
Passo 4
Com
Multiplicando por
Repara que , então, tanto quando é positivo
Isso vai nos dizer que
É sempre positivo.
Então a solução vai ser o nosso intervalo
Em forma de intervalo
Passo 5
Com
Multiplicando por
isso é uma função de segundo grau.
Vamos começar achando suas raízes
AS raízes vão ser
E
Como , o seu gráfico será algo assim
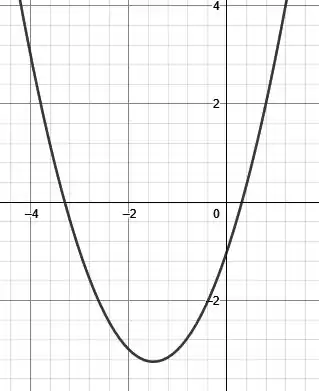
Entre as raízes é negativo e fora é positivo.
Como ele quer a parte negativa, vamos pegar
Nesse intervalo, temos que ele começa em , assim, vamos pegar só o intervalo da direita
Passo 6
Com
isso é uma função de segundo grau.
Vamos começar achando suas raízes
Opa, aquela raiz quadrada não existe nos reais.
Assim, como , vamos ter que a função é toda positiva
Como ele quer a parte negativa, não teremos solução aqui
Passo 7
Juntando tudo, vamos ter
Como
E queremos juntar os dois, a solução vai ser