Resolva em as seguintes inequações
Passo 1
Precisamos fazer os dos módulos e ver como será a expressão, primeiro vamos pegar
Resolvendo aquela inequação, vamos ter
E
Resultando em
Passo 2
Vamos para o segundo módulo
Resolvendo aquela inequação, vamos ter
E
Resultando em
E vamos ter
Passo 3
Vamos agora juntar todos esses módulos
Temos que olhar os intervalos primeiro, para entendermos como vai ficar
Então, no fundo temos
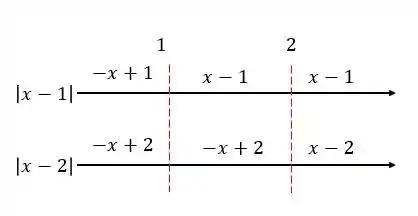
Fazendo a soma, vamos ter
Vai ficar
Vamos ter inequações para resolver em cada intervalo.
Passo 4
Com
Juntando isso com o intervalo que estamos, a solução aqui vai ser
Em forma de intervalo vai ser
Passo 5
Com
O que não é possível, então não temos nenhuma solução aqui
Passo 6
Com
Escrevendo ao contrário
Juntando isso com o intervalo que estamos, a solução aqui vai ser
Em forma de intervalo vai ser
Passo 7
Juntando os intervalos, vamos ter