Determine o domínio da seguinte função:
Passo 1
Para acharmos o domínio dessa função precisamos ver as restrições que ela tem. Repara que tem raiz quadradas ali né? Então queremos que o cara dentro de cada uma delas seja maior ou igual a . Além disso, temos uma expressão no denominador, neste caso queremos que ela seja diferente de .
Então para entender melhor as restrições, vamos primeiro analisar a parte e depois a parte .
Passo 2
Vamos começar com a parte,
E como mencionamos no Passo 1, o denominador não pode zerar. Com isso temos que,
Também foi comentado que dentro de cada raiz tem ser um valor maior ou igual a . Em outras palavras, nós temos essa restrição,
Mas do jeito que ela está escrita, está difícil de analisar quando ela vai respeitar essa condição. Então vamos dar uma arrumada nela para entender melhor. Para isso vamos aplicar um produto notável ali em cima,
Com isso, achamos duas restrições:
Agora vamos guarda essa informação, pois no fim vamos relembrar essas restrições para a resposta final.
Passo 3
Vamos para outra parte da função,
Seguimos com a restrição para raiz quadrada, ou seja, dentro dela tem que ser um valor maior ou igual a . Com isso temos que,
Para resolver essa parte, temos que fazer o gráfico e olhar como fica o sinal. Para fazer o gráfico precisamos:
- Achar as raízes dessa função
- Achar a concavidade dessa função
Vamos começar achando as raízes,
Assim vamos ter
Passo 4
Agora vamos para o segundo passo, que é achar a concavidade dessa função, repara que temos
Assim, como , essa função é côncava para cima
Passo 5
Beleza, agora que sabemos essas duas informações podemos fazer o esboço do gráfico. Quando fizemos gráfico antes nós completávamos o gráfico com os outros dois pontos importantes, mas como aqui só queremos ver o sinal, não vamos achar esses pontos porque são contas a mais.
O esboço do gráfico vai ficar
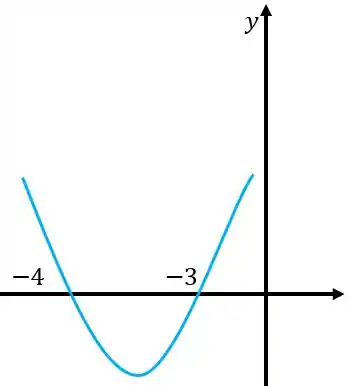
Podemos perceber então que entre as raízes ( e ), ele vai ser negativo, e na outra parte vai ser positivo, vamos deixar isso um pouco mais claro
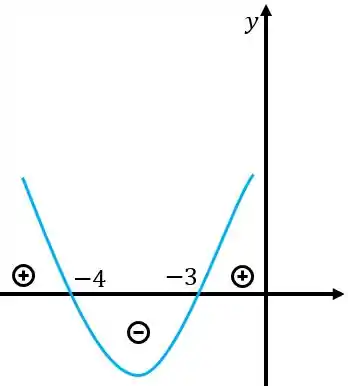
Beleza, achamos os sinais, agora vamos ver qual ele pede. Ele quer que essa função seja positiva para poder ter a raiz quadrada, assim, para essa parte precisamos ter
Passo 6
Pronto, chegou a hora de juntar todas as restrições que achamos!
Da primeira parte temos:
Da segunda parte temos:
Queremos que ele obedeça todas as condições! Repara que eu dei uma letrinha para cada restrição para facilitar nossa análise.
Vamos começar juntando e . Pois elas delimitam um intervalo que está inserido . Então podemos escrever assim,
Mas perai, olhando restrição , vemos que não pode ser e ele tá nesse intervalo. Então vamos dividir ele assim,
Repara que não colocamos o sinal igual para o Ele só pode ser menor ou maior que esse valor.
Por fim, vamos olhar para nossa restrição . Então, ela vai ficar como se fosse um buraco entre e no nosso domínio. Olha essa figura abaixo,
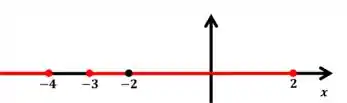
Escrevendo bonitinho matematicamente, ficamos com,