Seja
(a) Determine o domínio da função
(b) Determine as equações das retas assíntotas horizontais do gráfico de , caso existam
(c) Determine as equações das retas assíntotas verticais do gráfico de , caso existam.
(d) Sabendo que é crescente em todo o seu domínio, esboce abaixo o gráfico de e suas retas assíntotas, caos existam.
Passo 1
As assíntotas são curvas/retas que cruzam nosso gráfico, sem nunca chegar a tocar em nossa função, mesmo por mais próximas que elas possam ficar. Quando falamos de assíntotas verticas ou horizontais, então falando de retas que perseguem gráficos hiperbólicos
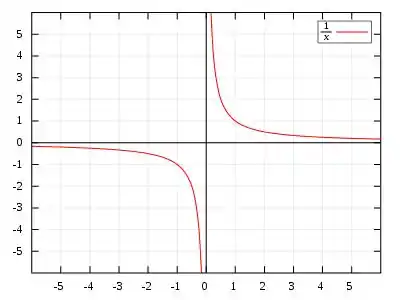
Na imagem acima, os eixos e são exemplos de assíntotas horizontais e verticas respectivamente.
Assim para analisarmos nossos limites laterais em busca de nossas assíntotas, devemos estudar, como nossa função de comporta nos seus limites extremos (discutiremos melhor no item referente). Perceba no gráfico que essa funções tendem a se comportar como uma reta. Reta essa que queremos escontrar posteriormente.
Passo 2
(a) O dóminio de uma função é o conjunto de pontos que podemos aplicar nosso valor .
Perceba que preciamos analisar 3 condições para os valores de . O primeiro termo “, e .
Analisando nossa função, observe que não há nenhum problema no primeiro termo .
O terceiro termos, temos que não pode ser zero, visto que
Agora para o segundo termo, temos que
Ou seja, para qualquer valor de nossa afirmação é verdadeira, visto que .
Agora para valores de , nossa afirmação é falsa, logo esses pontos não podem pertencer ao nosso domínio. Por fim, tome . Nesse intervalo, temos que nossa afirmação volta a ser verdadeira, com isso temos então
Desta forma, temos que nosso domínio
Uma outra forma de escrevermos nosso domínio é
Passo 3
(b) Queremos encontrar as assíntotas horizontais, assim perceba que ela deverá ser uma reta na qual tende a se aproximar da nossa curva quando .
Desta forma, tome
Onde se se aplicarmos o limite temos , então aplicamos .
Tomando agora para
Assim temos que nossa reta assíntota horizontal é dada por
Passo 4
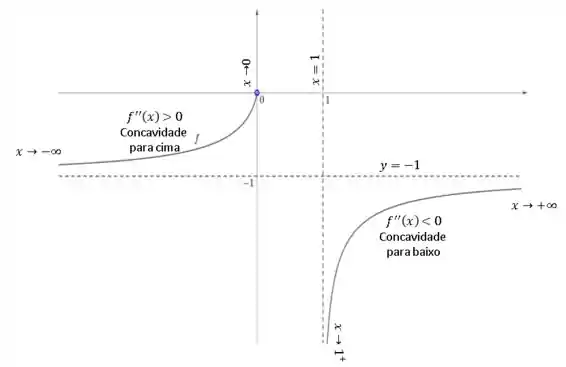
(c) Agora queremos encontrar a reta assíntota vertica. Olhando para o passo 1, temos em nosso gráfico (ilustrativo) que, quando nossa curva tente a , temos que nossa curva se aproxima de uma reta. Entretanto, nosso problema sugere que nossa reta se aproxima na verdade de (observe o domínio da nossa função) pela direita e pela esquerda.
Assim, analisando os limites, temos
E
Ou seja
Quando o se aproxima de pela esquerda (única situação válida – olhar domínio), nossa função tende ao ponto . Quando o tende a pela direita, nossa função explode para o infinito. Isso indica que ela nos temos nossa reta assíntota vertical.
Passo 5
Depois de tudo que vimos, tome que
Derivando e aplicando a regra do produto.
Com nossa dada por
E a derivada segunda, temos
Pela derivada primeira, já sabemos que não há pontos críticos, visto que nossa função só será nula nos extremos. Também sabemos que o não haverá pontos de inflexão, visto que nossa segunda derivada só será nula nos extremos novamente.
Agora a concavidade das nossas curvas são dadas pelo sinal da nossa derivada segunda. Perceba que
Ou seja, para a concavidade é para cima e para a concavidade é para baixo