Assinale somente as alternativas com afirmações corretas.

(Haverá desconto na nota desta questão caso alternativas incorretas sejam assinaladas.)

Escolha uma ou mais:

a) Se é uma função qualquer tal que , então existe tal que

b) Se e são função deriváveis definidas em e se em , então em

c) Se é uma função que admite derivada até segunda ordem em toda a reta, tal que e , então

d) Se e são polinômios, tais que grau(), então possui assíntotas vertical, ou seja, existe tal que ou

e) Se é uma função derivável até segunda ordem tal que tem duas soluções reais distintas, então tem algum ponto de extremo (máxima ou mínimo) local.

f) Se é uma função tal que para todo então .

Letra b) Falsa

Para provar que uma sentença é falsa, podemos encontrar um caso em que seja falso.

Usando as função e , suas derivadas vão ser: e .

Para vamos ter que , o que garante que nossa premissa seja verdadeira:

Porém para as derivadas temos e , o que é uma conclusão falsa.

Portanto nossa sentença é falsa.

Letra c) Verdadeira

Como temos que a primeira derivada é positiva, sabemos que nossa função vai ser estritamente crescente e como temos que a segunda derivada é positiva, a função vai ter concavidade para cima. Com isso podemos dizer que ela sempre vai crescer no sentido de , então:

Letra d) Falsa

Para provar que uma sentença é falsa, podemos encontrar um caso em que seja falso então nossa sentença vai ser falsa.

Usando as função e .

Podemos ver que grau() e assim vamos ter que não possui assíntota vertical nem horizontal.

Letra e) Falsa

Pra essa vou trazer um desenho maneiro que fiz no paint mesmo e quero que você aprecie comigo haha

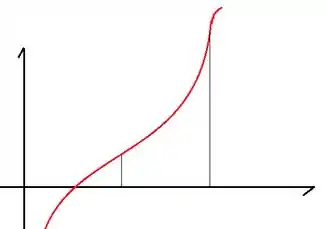
Observa como nessa dunção que desenhei temos duas mudanças de concavidade. Começamos virados para baixo, depois pra cima e depois ali no finalzinho pra baizo novamente. Em nenhum momento passamos necessariamente por um ponto de máximo e mínimo, mesmo tenhdo nossa segunda derivada com duas soluções.

Letra f) Verdadeira

Analisando .

Como temos que sempre será limitado por e qualquer que seja o se mostrarmos que , demonstraremos que a primeira igualdade é verdadeira.

Olhando agora para a desigualdade vamos aplicar o limite para os três termos.

O lado direito sabemos que da , falta agora vermos o lado esquerdo.

Não podemos aplicar L’Hôpital diretamente pois não temos uma indeterminação do tipo ou .

Fazendo:

Agora sim temos uma indeterminação em que podemos aplicar L’Hôpital.

Vamos ter então:

Portanto pelo teorema do confronto temos que . Podemos afirmar então que: