3) Considere a função .
a) Mostre que o domínio de é precisamente o intervalo fechado
b) Determine os pontos de máximo e mínimo absolutos de . Ainda, calcule os valores de máximo e mínimo da função .
Passo 1
Fala aí, galerinha! Tudo belezinha com vocês?
Bom, essa questão deu pra gente a função e pediu pra determinar qual era o seu domínio. Mas como fazemos isso?
Pra determinar o domínio de uma função precisamos procurar os valores de em que a função está definida. Ou seja, os valores que o pode assumir sem dar problema em nenhuma parte da função. E no nosso casa, temos uma parte da função que está dentro de uma raiz quadrada, e ali não podemos ter valores negativos, pois no conjunto dos números reais a raiz quadrada de números negativos não está definida.
Então esse será o plano, procurara os valores de que funcionam dentro da raiz. Ok?
Na letra b) o problema também pede pra gente determinar os ponto e valores de máximo e mínimo da função, e faremos isso lembrando que a derivada da função vai a zero nos pontos críticos, que são os pontos que podem ser de máximo ou mínimo. Show?
Vem que te mostro como fazer.
Passo 2
Começando pela letra a), vamos procurar o domínio da função fazendo
Com
Podemos reescrever como
Podemos separa aqui em duas condições
Ou
Para
Teremos
E
E para
Como temos um produto entre duas funções onde precisamos que o resultado seja maior ou igual a zero, teremos que fazer a análise de sinal já que e .
Então vamos construir a seguinte tabela. Perceba que:
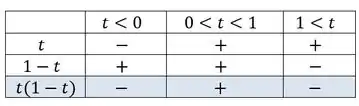
Juntando as duas informações que acabamos de encontrar, teremos o domínio constituído de valores de que podem ser
E pra ficar chique podemos escrever:
Maravilha, agora vamos para a letra b.
Passo 3
Para determinar os pontos de máximo e mínimo faremos a derivada da função igual a zero e acharemos os pontos críticos.
Como
Para fazer a derivada precisaremos usar a regra do produto, e da cadeia.
Assim
Ajeitando um pouco essa bagunça, teremos:
Vamos somar essas parcelas api usando o m.m.c.
Ficando com
Que pode ser escrito como:
Ou
Agora temos a derivada em forma de um produto. E estamos procurando os pontos críticos, então essa derivada será igual a zero. Vamos fazer isso no próximo passo, pra ficar tudo organizado na nossa cabeça.
Passo 4
Um produto só pode dar zero se um dos seus fatores for igual a zero. Assim:
Se
Mas aqui não podemos fazer , pois isso gera uma indeterminação. Só o que podemos concluir é que esse é um fator positivo.
Sim só teremos
Onde
Achamos nosso ponto crítico. Como se trata de um intervalo fechado, precisamos também avaliar o valor da função nesse ponto crítico e também nos extremos do intervalo.
Passo 5
Vamos calcular o valor da função em cada um dos pontos que temos para determinar seus pontos de máximo e mínimo.
Lembrado que o intervalo é fechado em
Assim, se
E
E poderemos dizer que e são mínimos absolutos de , e tem valor mínimo igual a .
E também que é ponto de máximo absoluto de , e tem valor máximo igual a .
E prontinho! Encontramos nossa resposta!
Resposta
a)
b)
Ponto de mínimo absoluto da função em e
Ponto de máximo absoluto da função em
Valor mínimo da função
Valor máximo da função