Considere a função , restrita ao intervalo .
Determine os subintervalos onde é crescente, assim como aqueles onde é decrescente.
Usando as informações do item anterior, determine os pontos de máximo e de mínimo de , indicando se são absolutos(globais) ou relativos(locais).
Passo 1
Oi, gente bonitaaaaaaa! Bora fazer mais um exercício?!
A questão deseja que determinemos quais são os subintervalos onde a função é crescente e em quais intervalos a função é decrescente. Sendo,
Essa função é limitada ao intervalo de .
Além disso, devemos também informar quais são os pontos de máximos e mínimos da função , e indicar se esses pontos são pontos globais ou locais.
Por onde começamos???
Passo 2
Meu povo, quando a função passa a ter um grau maior ou igual a é difícil conseguirmos imaginar com nitidez o gráfico da função. Tá, mais precisamos então determinar em que intervalos essa função cresce e decresce sem precisar desenhar essa função . E agora?
Calmaaa! Nem tudo está perdido hahaha
Como a derivada de uma função indica a angulação da reta tangente a cada ponto da curva, podemos utilizar desse recurso matemático para analisar em que momento a função cresce e em que momento ela decresce.
Sendo assim,
Colocando o em evidência...
Então, agora precisamos fazer a análise do sinal desse produto tal qual fazíamos quando estudamos inequações.
Para :
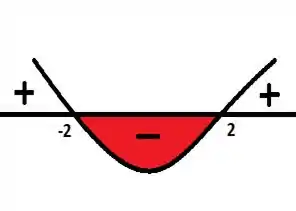
E agora para :
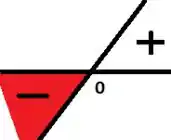
Passo 3
Com as imagens anteriores conseguimos montar uma tabelinha de estudo do sinal para a derivada :
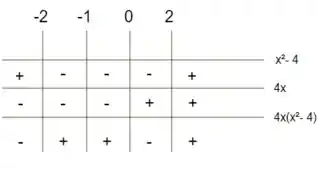
Ótimo! Só que preciso lembrar aos senhores (as) que a nossa função é limitada ao intervalo de . Portanto, o estudo do sinal da nossa derivada também será limitado a esse intervalo.
Logo vemos que
A nossa função é crescente para os subintervalos:
e
E decrescente para o intervalo de
Galerinha! Reforçando, quando a derivada é positiva significa que a nossa função está crescendo. Já quando a derivada é negativa significa que a nossa função está decrescendo. Uma vez que a derivada representa o coeficiente angular da reta tangente à curva.
Passo 4
Show! Agora vamos dar uma olhadinha no gráfico dessa função.
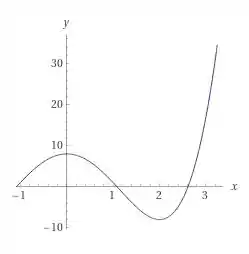
Então vemos que super confere os resultados que chegamos até aqui. Agora precisamos determinar quais são os pontos de máximos e mínimos da função e quais são os pontos globais e quais são locais.
Antes, é necessário que compreendamos o que são pontos globais e o que são pontos locais.
Os pontos de máximos e mínimos locais são pontos de derivada igual a zero, ou seja, pontos críticos que assumem os valores máximos/ou mínimos dentro de um determinado intervalo.
Olhando o gráfico acima podemos afirmar que o ponto é um ponto de máximo local e que o ponto é um ponto de mínimo local.
Já os pontos de máximos/ mínimos globais são os extremos do nosso conjunto imagem, ou seja, é o maior e o menor valor que a nossa função pode assumir. Dessa forma, concluímos que temos um ponto de mínimo global e para temos um ponto de máximo global, uma vez que a função só aumenta depois de e é limitada ao intervalo de .
Resposta
Resolução nos passos acima