Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Máximos e Mínimos

Ver Teoria
Exercício 365123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 7 - Máximos e Mínimos, Questão 1.3b

1.3. Determine o valor máximo e o valor mínimo de f na região R sendo

b. f x , y , z = x 2 + y 2 + 2 z 2 - 4 x y - 4 z + 3 x e R = x , y , z ∈ R 3 : x + y + z ≤ 4   e   x , y , z ≥ 0 ;

Passo 1

Fala aí!! Bem-vindo! Está um pouco complicada essa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nesse problema queremos obter os pontos máximos e mínimos da função f x , y , z = x 2 + y 2 + 2 z 2 - 4 x y - 4 z + 3 x dentro da região R limitada pelo tetraedro x + y + z ≤ 4 com x , y , z ≥ 0 .

Parece de boa? 👀

Nesses casos, quando temos que obter os pontos máximos e mínimos podemos seguir uns passos...

Primeiro calculamos os pontos críticos de f normalmente e verificamos se esses pontos estão dentro da região R ... caso eles não estiverem, descartamos.

Depois calculamos os pontos críticos nas bordas da região pelo substituindo as superfícies em f e obtendo os pontos críticos.

Sacou? Bora começar! 😉

Passo 2

Primeiro vamos calcular o gradiente de f e igualá-lo a 0 .

f x = ∂ x 2 + y 2 + 2 z 2 - 4 x y - 4 z + 3 x ∂ x = 2 x - 4 y + 3

f y = ∂ x 2 + y 2 + 2 z 2 - 4 x y - 4 z + 3 x ∂ y = 2 y - 4 x

f z = ∂ x 2 + y 2 + 2 z 2 - 4 x y - 4 z + 3 x ∂ z = 4 z - 4

Portanto o gradiente de f é dado por

∇ f = 2 x - 4 y + 3 , 2 y - 4 x , 4 z - 4

Igualando a um vetor nulo

∇ f = 0 →

2 x - 4 y + 3,2 y - 4 x , 4 z - 4 = 0,0 , 0

2 x - 4 y + 3 = 0 2 y - 4 x = 0 4 z - 4 = 0 → x = 4 y - 3 2 x = y 2 z = 1

Igualando as duas primeiras equações

4 y - 3 2 = y 2

4 y - 3 = y

y = 1

Portanto, se x = y 2

x = 1 2

Dessa forma, encontramos um ponto crítico de f dado por P 1 = 1 2 , 1,1 .

Para saber se esse ponto faz parte de R , substituímos na equação da restrição

x + y + z ≤ 4 → 1 2 + 1 + 1 ≤ 4

5 2 ≤ 4

A inequação foi satisfeita, portanto esse ponto é válido.

Tranquilo até aqui? 👀

Passo 3

Agora vamos analisar as bordas da região R

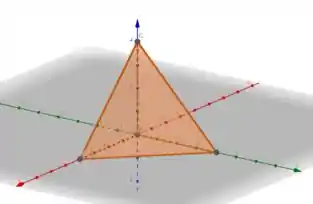
No caso, temos quatro superfícies que limitam nossa região...

x = 0 y = 0 z = 0 x + y + z = 4

Para a superfície x = 0 , temos

f 0 , y , z = 0 2 + y 2 + 2 z 2 - 4 0 y - 4 z + 3 0

f y , z = y 2 + 2 z 2 - 4 z

Calculando o gradiente e igualando a 0

∇ f = ∂ f ∂ y , ∂ f ∂ z = ∂ y 2 + 2 z 2 - 4 z ∂ y , ∂ y 2 + 2 z 2 - 4 z ∂ z

∇ f = 2 y , 4 z - 4 = 0,0

y = 0

z = 1

Assim encontramos mais um ponto a ser estudado...

P 2 = 0,0 , 1

Bacana, não é? 😬

Passo 4

Agora vamos verificar os pontos críticos sobre o plano y = 0

f x , 0 , z = x 2 + 0 2 + 2 z 2 - 4 x 0 - 4 z + 3 x

f x , z = x 2 + 2 z 2 - 4 z + 3 x

Calculando o gradiente de f

∇ f = ∂ f ∂ x , ∂ f ∂ z = ∂ x 2 + 2 z 2 - 4 z + 3 x ∂ x , ∂ x 2 + 2 z 2 - 4 z + 3 x ∂ z

∇ f = 2 x + 3 , 4 z - 4 = 0,0

x = - 3 2

z = 1

Como temos que ter x , y e z ≥ 0 , esse ponto que encontramos não faz parte da região R .

Agora faremos o mesmo para a superfície z = 0

f x , y , 0 = x 2 + y 2 + 2 0 2 - 4 x y - 4 0 + 3 x

f x , y = x 2 + y 2 - 4 x y + 3 x

Obtendo o gradiente de f

∇ f = ∂ f ∂ x , ∂ f ∂ y = ∂ x 2 + y 2 - 4 x y + 3 x ∂ x , ∂ x 2 + y 2 - 4 x y + 3 x ∂ y

∇ f = 2 x - 4 y + 3 , 2 y - 4 x = 0.0

2 x - 4 y + 3 = 0

2 y - 4 x = 0 → y = 2 x

Substituindo na primeira equação

2 x - 4 2 x + 3 = 0 → 2 x - 8 x + 3 = 0

x = 1 2

Assim, o próximo ponto é dado por

P 3 = 1 2 , 1,0

Está acompanhando? 👀

Passo 5

Agora nos aproximando pelo plano x + y + z = 4

z = 4 - x - y

Substituindo em f

f x , y , 4 - x - y = x 2 + y 2 + 2 4 - x - y 2 - 4 x y - 4 4 - x - y + 3 x

f x , y = x 2 + y 2 + 2 x 2 - 8 x - 8 y + 2 x y + y 2 + 16 - 4 x y - 16 + 4 x + 4 y + 3 x

f x , y = x 2 + y 2 + 2 x 2 - 16 x - 16 y + 4 x y + 2 y 2 + 32 - 4 x y - 16 + 4 x + 4 y + 3 x

f x , y = 3 x 2 + 3 y 2 - 9 x - 1 2 y + 16

Calculando o gradiente...

∇ f = ∂ f ∂ x , ∂ f ∂ y = ∂ 3 x 2 + 3 y 2 - 9 x - 12 y + 16 ∂ x , ∂ 3 x 2 + 3 y 2 - 9 x - 12 y + 16 ∂ y

∇ f = 6 x - 9 , 6 y - 12 = 0,0

6 x - 9 = 0 → x = 3 2

6 y - 12 = 0 → y = 2

Substituindo x e y em z ...

z = 4 - 3 2 - 2 = 1 2

Assim, encontramos mais um ponto dado por

P 4 = 3 2 , 2 , 1 2

Estamos quase no fim! 😉

Passo 6

Agora o que resta é obter a imagem desses pontos que encontramos e dos vértices P 5 = 4,0 , 0 , P 6 = 0,4 , 0 , P 7 = 0,0 , 4 e P 8 = 0,0 , 0 e verificar qual é maior e qual é menor

f x , y , z = x 2 + y 2 + 2 z 2 - 4 x y - 4 z + 3 x

Para o ponto P 1 = 1 2 , 1,1 , temos

f P 1 = 1 2 2 + 1 2 + 2 1 2 - 4 1 2 1 - 4 1 + 3 1 2 = - 5 4

Para o ponto P 2 = 0,0 , 1  

f P 2 = 0 2 + 0 2 + 2 1 2 - 4 0 0 - 4 1 + 3 0 = - 2

Para o ponto P 3 = 1 2 , 1,0  

f P 3 = 1 2 2 + 1 2 + 2 0 2 - 4 1 2 1 - 4 0 + 3 1 2 = 3 4

E para o ponto P 4 = 3 2 , 2 , 1 2

f P 4 = 3 2 2 + 2 2 + 2 1 2 2 - 4 3 2 2 - 4 1 2 + 3 3 2 = - 11 4

Agora para os vértices, começando por P 5 = 4,0 , 0

f P 5 = 4 2 + 0 2 + 2 0 2 - 4 4 0 - 4 0 + 3 4 = 28

Por P 6 = 0,4 , 0

f P 6 = 0 2 + 4 2 + 2 0 2 - 4 0 4 - 4 0 + 3 0 = 16

Para P 7 = 0,0 , 4

f P 7 = 0 2 + 0 2 + 2 4 2 - 4 0 0 - 4 4 + 3 0 = 16

E por último, P 8 = 0,0 , 0

f P 8 = 0 2 + 0 2 + 2 0 2 - 4 0 0 - 4 0 + 3 0 = 0

Comparando os resultados, vemos que no ponto P 5 = 4,0 , 0 a imagem de f foi máxima, f P 5 = 28 , já no ponto P 4 = 3 2 , 2 , 1 2 a imagem de f foi mínima f P 4 = - 11 4

É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta

No ponto P 5 = 4,0 , 0 a imagem de f foi máxima, f P 5 = 28 , já no ponto P 4 = 3 2 , 2 , 1 2 a imagem de f foi mínima f P 4 = - 11 4

Exercícios de Livros Relacionados

O gráfico da derivada f ' de uma função f está mostrado. (a) Em quais intervalos f é crescente ou decrescente? (b) Em que valores de x a função f tem um mínimo ou máximo local?
Encontre os números críticos da funçãof (x) = 5 x^2 + 4 x
Encontre os valores de máximo e mínimo absoluto de f no intervalo dado f x = 3 x 2 - 12 x + 5 ,[ 0,3 ]
É dada uma fórmula para a derivada de uma função. Quantos números críticos ela tem? f ' x = 100 cos 2 ⁡ x 10 + x 2 - 1
Encontre os números críticos da funçãoh (p) = (p - 1)/(p^2 + 4)