Encontre todos os pontos de máximos, mínimos ou pontos de sela da função:
Passo 1
Olá, tudo certo? O problema nos dá essa função aqui
E pede todos os pontos de máximos, mínimos ou pontos de sela. Mas você lembra como encontrar esses pontos?
Estamos falando de pontos críticos! Pontos críticos são onde as derivadas parciais (no nosso caso e ) são nulas!
E para classificar esses pontos, precisamos encontrar o determinante da matriz Hessiana:
Temos três opções para classificar o ponto :
- Se :
- Se temos que é ponto de sela
- Se o teste é inconclusivo
Então a ideia aqui é calcular as derivadas parciais e igualar a zero, o que vai dar num sistema que a gente precisa resolver. Disso vamos achar os pontos críticos! Aí com esses pontos é #partiu classificação!
Belezinha até aqui?

Mas relaxa, vou fazer junto com você!
Passo 2
Nossa função é a seguinte
Vamos relembrar que pra calcular derivadas parciais com relação a uma variável, todas as outras se comportam como constantes.
Calculando e igualando a zero temos
Como para qualquer valor de , então esse produto só será zero se
Beleza? Vamos guardar esse resultado! Vamos agora calcular e depois combinar os resultados:
Novamente, se a exponencial nunca é zero, então é o seno que vai ser zero. Logo
Agora vamos combinar esses resultados!
Percebe que não temos um sistema? Encontramos apenas valores de ! Então a derivada só será nula na direção de quando
E na direção de quando
Mas repara que esses 2 resultados não têm nada em comum, ou seja, a derivada nunca vai ser zero nas duas direções.
Quando temos que a derivada é zero em apenas uma das direções, chamamos esse ponto de ponto de sela!
Mas para verificar isso, vamos precisar calcular ! (teste da derivada segunda) bora?
Passo 3
Para classificar precisamos encontrar aquele
Então vamos precisar das derivadas de segunda ordem!
Do passo :
Derivando novamente
Assim é
Beleza? E como a exponencial é sempre positiva:

Vamos dar uma olhada no gráfico dessa função?
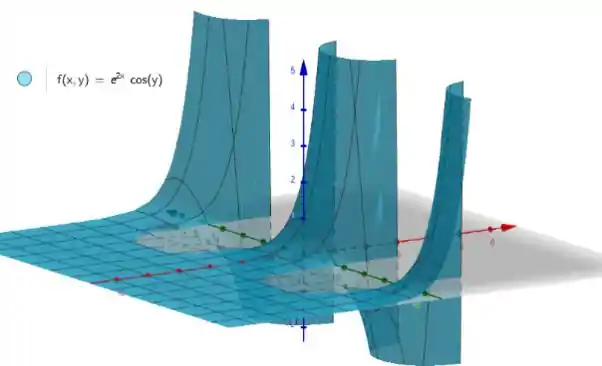
Temos repetidos pontos de sela! Isso porque temos uma parte periódica na função! Então nossos pontos de sela são
Na direção de :
E na direção de quando
E é isso galera! Vamos para a próxima?