Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Máximos e Mínimos

Ver Teoria
Exercício 357123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 7 - Máximos e Mínimos, Questão 1.1d

1.1. Esboce a região D e determine o máximo e o mínimo absolutos da função f : D → R quando

d. f x , y = 2 x 3 + y 4 e D = x , y ∈ R 2 : x 2 + y 2 = 1 , x ∈ 0 , 1 4 , y ≥ 0 .

Passo 1

Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉

Nesse problema queremos obter os pontos máximos e mínimos da função f x , y = 2 x 3 + y 4 dentro da região D limitada pela circunferência x 2 + y 2 = 1 em que x ∈ 0 , 1 4 e y ≥ 0 .

Parece de boa? 👀

Nesses casos, quando temos que obter os pontos máximos e mínimos podemos seguir uns passos...

Primeiro calculamos os pontos cr��ticos de f normalmente e verificamos se esses pontos estão dentro da região D ... caso eles não estiverem, descartamos.

Depois calculamos os pontos críticos nas bordas da região substituindo as equações que limitam D na função f .

Sacou? Bora começar! 😉

Passo 2

Primeiro vamos obter a região D

Esboçando a circunferência e hachurando a região entre x = 0 e x = 1 / 4 onde y ≥ 0 , temos

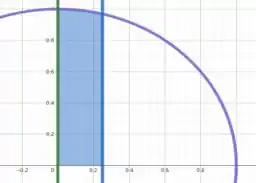
Primeiro vamos obter os pontos críticos gerais da função para saber se há algum na região interna a D .

Obtendo a derivada parcial de f em x ...

f x = ∂ 2 x 3 + y 4 ∂ x = 6 x 2 = 0

x = 0

Agora com relação a y

f y = ∂ 2 x 3 + y 4 ∂ y = 4 y 3 = 0

y = 0

Portanto, a função f possui um ponto crítico situado em P 1 = 0,0 sendo exatamente um vértice da nossa região D .

Tranquilo até aqui? 😁

Passo 3

Agora vamos começar a analisar as curvas que limita, nossa região...

Começando por x = 0 , temos

f 0 , y = 2 0 3 + y 4 → f y = y 4

Calculando os pontos críticos dessa função...

f y = 4 y 3 = 0 → y = 0

Já tínhamos encontrado o ponto 0,0 antes, então podemos desconsiderá-lo agora.

Agora para a curva y = 0

f x , 0 = 2 x 3 + 0 4 → f x = 2 x 3

f x = 6 x 2 = 0 → x = 0

Novamente encontramos o mesmo ponto...

Agora pela reta x = 1 4

f 1 4 , y = 2 1 4 3 + y 4 → f y = 1 32 + y 4

f y = 4 y 3 = 0 → y = 0

Agora encontramos o ponto P 2 = 1 4 , 0 que é outro vértice de D .

Por último fazemos para a curva x 2 + y 2 = 1 → y = 1 - x 2

f x , 1 - x 2 = 2 x 3 + 1 - x 2 4

f x = 2 x 3 + 1 - x 2 2

f x = 2 x 3 + 1 - 2 x 2 + x 4

f x = x 4 + 2 x 3 - 2 x 2 + 1

Derivando essa função e igualando a 0

f x = 4 x 3 + 6 x 2 - 4 x = 0

x 4 x 2 + 6 x - 4 = 0

x = 0 x = 1 2 x = - 2

Dessas coordenadas, a única que pertence a D é x = 0 .

Bacana, não é? 😐

Passo 4

Em resumo da opera, os únicos pontos críticos que obtemos até agora coincidiram exatamente com os vértices da região D , ou seja

P 1 = 0,0

P 2 = 0,1

P 3 = 1 4 , 15 4

P 4 = 1 4 , 0

Só nos resta obter as imagens desses pontos em f e verificar qual é maior e qual é menor

Para P 1

f 0,0 = 2 0 3 + 0 4 = 0

Para P 2

f 0,1 = 2 0 3 + 1 4 = 1

Para P 3

f 1 4 , 15 4 = 2 1 4 3 + 15 4 4 = 233 256

Para P 4

f 1 4 , 0 = 2 1 4 3 + 0 4 = 1 32

Logo, vemos que P 1 = 0,0 é o ponto mínimo com f 0,0 = 0 e P 2 = 0,1 é o ponto máximo em que f 0,1 = 1 .

Sacou como faz? Responde Aí! 😉

Resposta

P 1 = 0,0 é o ponto mínimo com f 0,0 = 0 e P 2 = 0,1 é o ponto máximo em que f 0,1 = 1 .

Exercícios de Livros Relacionados

O gráfico da derivada f ' de uma função f está mostrado. (a) Em quais intervalos f é crescente ou decrescente? (b) Em que valores de x a função f tem um mínimo ou máximo local?
Encontre os números críticos da funçãof (x) = 5 x^2 + 4 x
Encontre os valores de máximo e mínimo absoluto de f no intervalo dado f x = 3 x 2 - 12 x + 5 ,[ 0,3 ]
É dada uma fórmula para a derivada de uma função. Quantos números críticos ela tem? f ' x = 100 cos 2 ⁡ x 10 + x 2 - 1
Encontre os números críticos da funçãoh (p) = (p - 1)/(p^2 + 4)