Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 124123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 3, Lista de Exercícios - USP - Lista 1 - 2022.1, Questão 14a

  1. Calcule a massa de D   =   { ( x , y ) : x - 2 y + 3 2 + 3 x + 4 y - 1 2 ≤ 100 } , com função densidade δ x , y = x - 2 y + 18 .

Passo 1

Olá meu amigo, o que sabemos é que para calcularmos a massa de uma região com densidade δ utilizamos a integral,

m = ∫ ∫ D δ x , y d A

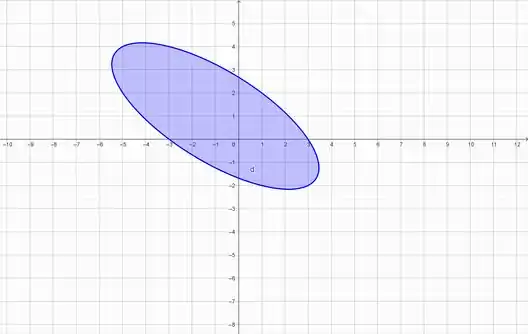
A região D pode ser vista abaixo em um gráfico gerado no Geogebra,

Passo 2

Para calcularmos essa integral, o melhor a se fazer e realizarmos uma substituição de x , y → ( r , θ ) . Então temos,

{ x - 2 y + 3 = r cos ⁡ θ 3 x + 4 y - 1 = r sin ⁡ θ

{ x = 2 r cos ⁡ θ + r sin ⁡ θ 5 - 1 r sin ⁡ θ - 3 r cos ⁡ θ 10 + 1

Temos que calcular o ∂ x , y ∂ r ,   θ quando realizamos substituições do tipo, então

| det ⁡ 2 5 cos ⁡ θ + 1 5 sin ⁡ θ - 2 r sin ⁡ θ + r cos ⁡ θ 5 sin ⁡ θ - 3 cos ⁡ θ 10 r cos ⁡ θ + 3 r sin ⁡ θ 10 |

| 1 50 [ 2 r cos 2 ⁡ θ + 6 r cos ⁡ θ sin ⁡ θ + r cos ⁡ θ sin ⁡ θ + 3 r sin 2 ⁡ θ - - 2 r sin 2 ⁡ θ + 6 r sin ⁡ θ cos ⁡ θ + r cos ⁡ θ sin ⁡ θ - 3 r cos 2 ⁡ θ ]

∂ x , y ∂ r ,   θ = 1 50 5 r cos 2 ⁡ θ + 5 r sin 2 ⁡ θ = r 10 = r 10

Passo 3

Agora poderemos começar a montar nossa integral e começarmos a calcula-la,

m = ∫ ∫ D δ x , y d x d y

= ∫ ∫ D δ r , θ ∂ x , y ∂ r ,   θ d r d θ

δ r , θ = x - 2 y + 18 = x - 2 y + 3 + 15 = r cos ⁡ θ + 15

Temos como restrição, que

D r ,   θ = r , θ ϵ 0 ≤ r ≤ 10 }

Finalmente montando nossa integral,

m =   ∫ 0 2 π ∫ 0 100 r cos ⁡ θ + 15 ∙ r 10 d r d θ = 1 10 ∫ 0 2 π ∫ 0 10 r 2 cos ⁡ θ + 15 r d r d θ

= 1 10 ∫ 0 2 π ( 10 3 3 cos ⁡ θ + 15 2 10 2 ) d θ

= 1 10 10 3 3 ∙ 0 + 15 2 ∙ 10 2 ∙ 2 π = 150 π

Resposta

150 π

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}