UFMG – Cálculo 3 – P1 – 2022/2
3) Calcule o valor da integral
Onde é a região delimitada pelas curvas e .
Passo 1
Falaaa... tudo belezinha??
Nessa questão vamos calcular essa integral feiosa, mas vamos se formos resolver do jeito convencional vai ser beeem difícil ou, até, impossível.
O que vai nos ajudar nessa questão é a mudança de variáveis. Como temos e talss já é uma dica de que vamos usar coordenadas polares.
Onde é o jacobiano. Uma parcela que sempre precisamos multiplicar quando fazemos mudança de variável.
Passo 2
Vamos primeiro fazer um esboço dessa região pra definir os limites de integração:
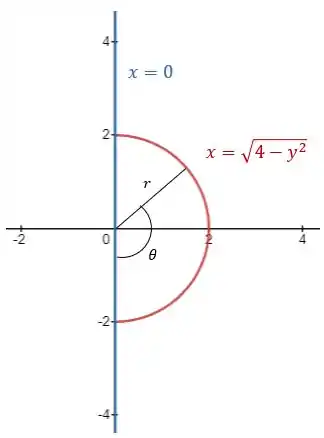
Temos que varia de -2 a 2 e que varia de 0 a .
Então a integral fica:
Passo 3
Agora vamos fazer essa bendita mudança de variável.
Para coordenadas polares, temos:
E precisamos calcular o jacobiano:
E já vamos dar uma olhada lá na figura da região pra achar os novos limites de integração.
Repara que varia de zero a 2 e que varia de a .
Com a mudança de variável, ficamos com:
Passo 4
Resolvendo a integral de dentro por substituição simples:
Chamamos:
Para os limites de integração:
Ohh... acabamos mais uma. Partiu pra próxima?