Considere a integral dupla em coordenadas polares:
a) Esboce a região de integração no plano cartesiano.
Sugestão: Analise a imagem das retas .
b) Calcule e interprete geometricamente a integral .
Passo 1
a)
Antes de tudo, vamos lembrar como que é a transformação para coordenadas polares:
No enunciado ele dá uma sugestão de analisar a imagem das retas para valores de específicos, mas sinceramente não acho que essa seja a melhor forma de fazer, que além de ser trabalhosa, não deixa nada muito claro. Então vou só analisar os limites da integral e ver o que podemos tirar disso.
Passo 2
Primeiro, nós temos que , isso nos diz que , já que é sempre positivo nesse intervalo.
Agora, temos que começa em , então sabemos que a regiao vai da origem, até . Mas se lembrarmos que:
Então podemos escrever esse limite assim:
Que, completando quadrados nos leva a:
Que é simplesmente a equação de uma circunferência centrada em e raio .
Graficamente, vamos ficar com isso:
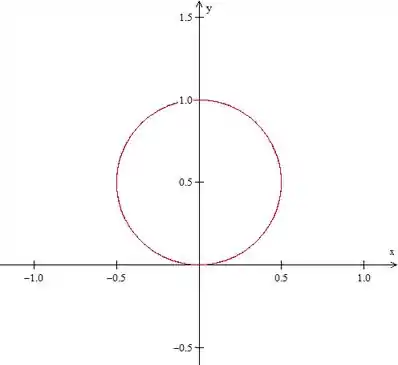
Passo 3
b)
Bem, vamos logo calcular a integral:
Se lembrarmos que :
Passo 4
O que ele quis dizer para interpretarmos geometricamente é que temos que reparar que é a área () da circunferência de raio , o que faz bastante sentido se lembrarmos que, com coordenadas polares , então teriamos:
Resposta
a)
b) , a área da região.