Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 128123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFSCAR, Sem Campus, Cálculo 3, Listas de C3 - Profª Alessandra Verri - Lista 3, Questão 1a

Exercício 1. Por meio de coordenadas polares, calcule a integral

(a) ∫ ∫ R x 2 + y 2 3 2 d A , em que R é a região limitada pelo círculo x 2 + y 2 = 4 .

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nesse problema queremos calcular a integral ∫ ∫ R x 2 + y 2 3 2 d A em que R é a região limitada por x 2 + y 2 = 4 . Pra isso temos que usar coordenadas polares!

Tem ideia de como fazer isso? 🤔

Fazemos esse tipo de conversão quando temos alguma simetria polar na região de integração da integral, como nesse caso em que a região R é limitada por x 2 + y 2 = 4 .

Para fazer a conversão de coordenadas cartesianas para coordenadas polares temos que fazer x = r cos ⁡ θ e y = r sin ⁡ θ .

Para completar a conversão, multiplicamos a função de integração por r e definimos os limites de integração em função de r e θ .

Bacana, não é? Bora começar! 😉

Passo 2

Vamos começar convertendo nossa função de integração...

f x , y = x 2 + y 2 3 2

Fazendo x = r cos ⁡ θ e y = r sin ⁡ θ .

f r , θ = r cos ⁡ θ 2 + r sin ⁡ θ 2 3 2

f r , θ = r 2 cos 2 ⁡ θ + r 2 sin 2 ⁡ θ 3 2

f r , θ = r 2 cos 2 ⁡ θ + sin 2 ⁡ θ 3 2

Sabemos que cos 2 ⁡ θ + sin 2 ⁡ θ = 1 , logo

f r , θ = r 2 3 2

f r , θ = r 3

Agora vamos definir os limites de integração... pra isso vamos analisar a região R .

Como a circunferência x 2 + y 2 = 4 limita nossa região R podemos perceber que r varia de 0 a 2 e θ de 0 a 2 π .

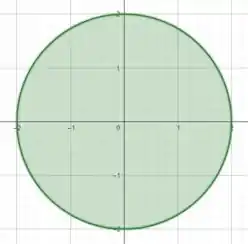
Tranquilo até aqui? 😊

Passo 3

Agora vamos substituir essas informações na integral

∫ ∫ R x 2 + y 2 3 2 d A → ∫ 0 2 π ∫ 0 2 r 3 · r d r d θ

∫ 0 2 π ∫ 0 2 r 4 d r d θ

Integrando em relação a r , temos

∫ r 4 d r = r 5 5

Aplicando os limites de integração

∫ 0 2 r 4 d r = 2 5 5 - 0 5 5

∫ 0 2 r 4 d r = 32 5

Integrando o resultado em função de θ , chegamos em

∫ 32 5 d θ = 32 5 θ

Aplicando os limites de integração.

∫ 0 2 π 32 5 d θ = 32 5 2 π - 32 5 0

∫ 0 2 π 32 5 d θ = 64 π 5

Portanto, chegamos que

∫ ∫ R x 2 + y 2 3 2 d A = 64 π 5

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

∫ ∫ R x 2 + y 2 3 2 d A = 64 π 5

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}