Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Mudança para Coordenadas Polares

Ver Teoria
Exercício 103123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFJF. Cálculo 3. Lista de Estudos. Lista da AV1 – 2022.2. Questão 1.

1. Seja R a região limitada pelas curvas y = 3 x , y = x , x = 1 e x = 2 . Mude a integral ∬ R 1 x 2 + y 2 d x d y para coordenadas polares.

Passo 1

Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍

Nessa questão, temos uma integral dupla dada por

∬ R 1 x 2 + y 2 d x d y

Sendo R a região de integração limitada pelas equações y = 3 x , y = x , x = 1 e x = 2 .

Nosso objetivo aqui é converter nossa integral para coordenadas polares para calcular o seu resultado.

Como podemos começar esse problema? 🤔🤔

A primeira coisa que temos que fazer é esboçar a região de integração para observarmos a região R e obter os limites de integração.

Depois disso, fazemos a conversão das coordenadas retangulares x y para as coordenadas polares r θ .

Entendeu? Bora para o cálculo! 😁

Passo 2

Primeiro vamos esboçar as curvas y = 3 x , y = x , x = 1 e x = 2 . Assim, vamos obter a região de integração. (a escala da imagem está 1 para x e 2 para y )

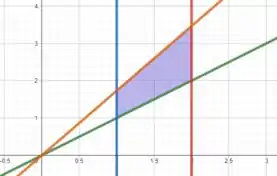
Com isso podemos observar que nossa região varia de x = 2 para x = 1 (horizontalmente) e de y = 3 x para y = x (verticalmente).

Quando convertemos um sistema para coordenadas polares, estamos reescrevendo x como r c o s θ e y como r s e n θ .

Reescrevendo as equações que limitam nossa região, começando por x = 2 , temos

x = 2

r c o s θ = 2

r = 2 cos ⁡ θ

Agora para x = 1 , temos

x = 1

r c o s θ = 1

r = 1 cos ⁡ θ

Portanto, agora não dizemos mais que horizontalmente a região varia de x = 2 para x = 1 , agora dizemos que o raio varia entre 2 cos ⁡ θ e 1 cos ⁡ θ .

Entendeu? 👀

Passo 3

Agora fazemos o mesmo para as equações que limitam nossa região verticalmente y = 3 x e y = x .

Para y = 3 x

r s e n θ = 3 r c o s θ

Simplificando r

s e n θ = 3 c o s θ

s e n θ c o s θ = 3

Podemos fazer uma relação trigonométrica aqui que é s e n θ c o s θ = t g θ

t g θ = 3

θ = t g - 1 3

θ = π 3

Agora para a equação x = y

r s e n θ = r c o s θ

s e n θ = c o s θ

s e n θ c o s θ = 1

Aplicando a mesma relação

t g θ = 1

θ = t g - 1 1

θ = π 4

Com esses achados, não dizemos mais que nossa região varia entre y = 3 x e y = x verticalmente. Agora dizemos que θ varia entre π 3 e π 4 .

Tranquilo até aqui? 😁

Passo 4

Nessa etapa, convertemos nossa integral de d x d y para d r d θ , sem esquecer do jacobiano r !

Como x = r c o s θ e y = r s e n θ , podemos afirmar que x 2 + y 2 = r 2 .

Essa relação vem muito a calhar pois nossa integral é dada por

∬ R 1 x 2 + y 2 d x d y

Fazendo essa substituição e adicionando o jacobiano à função de integração

∬ R 1 r 2 r d r d θ

Simplificando...

∬ R 1 r r d r d θ

∬ R 1 d r d θ

Adicionando os limites de integração na integral, temos

∫ π 4 π 3 ∫ 1 cos ⁡ θ 2 cos ⁡ θ 1 d r d θ

Vamos calcular essa integral!

Primeiro com relação a d r , é simples pois nossa função de integração é uma constante e sabemos que a integral de uma constante é o produto da constante com a variável de integração.

∫ 1 d r = r

Aplicando os limites de integração

∫ 1 cos ⁡ θ 2 cos ⁡ θ 1 d r = 2 cos ⁡ θ - 1 cos ⁡ θ = 1 cos ⁡ θ

Podemos usar outra relação trigonométrica para esse resultado que diz que 1 cos ⁡ θ = sec ⁡ θ , ou seja

∫ 1 cos ⁡ θ 2 cos ⁡ θ 1 d r = sec ⁡ θ

Interessante, não é? 😎

Passo 5

Com esse resultado, nossa integral fica como

∫ π 4 π 3 sec ⁡ θ d θ

Aplicando as regras de integração para funções trigonométricas, vemos que a integral se sec ⁡ θ é dada por ln ⁡ t g θ + sec ⁡ θ , ou seja

∫ sec ⁡ θ d θ = ln ⁡ t g θ + sec ⁡ θ

Aplicando os limites de integração, vamos obter

∫ π 4 π 3 sec ⁡ θ d θ = ln ⁡ t g π 3 + sec ⁡ π 3 - ln ⁡ t g π 4 + sec ⁡ π 4

Calculando os resultados dessas funções trigonométricas, temos

t g π 3 = 3 sec ⁡ π 3 = 2 t g π 4 = 1 sec ⁡ π 4 = 2

∫ π 4 π 3 sec ⁡ θ d θ = ln ⁡ 3 + 2 - ln ⁡ 1 + 2

Usando uma propriedade dos logaritmos que diz que ln ⁡ a - ln ⁡ b = ln ⁡ a b , ou seja

∫ π 4 π 3 sec ⁡ θ d θ = ln ⁡ 3 + 2 1 + 2

Portanto, a integral de 1 x 2 + y 2 na região R resulta em

∬ R 1 x 2 + y 2 d x d y = ln ⁡ 3 + 2 1 + 2

É isso! Essa resolução te ajudou? Responde Aí! ✌

Resposta

∬ R 1 x 2 + y 2 d x d y = ln ⁡ 3 + 2 1 + 2

Exercícios de Livros Relacionados

Determine todos os valores de p para os quais I p , a tem um limite finito quando a tende para + ∞ .
Se a0 , seja I (a) = int_(- a)^a e^(- u^2) d u .Mostre queI^2 (a) = int int_D e^(- (x^2 + y^2)) d x d y Onde:D = [- a , a] xx [- a , a]
Se a0 , seja I a = ∫ - a a e - u 2 d u .Se B 1 e B 2 são bolas inscrita e circunscrita a D , respectivamente mostre que ∫ ∫ B 1 e - x 2 + y 2 d x d y ≤ I 2 a ≤ ∫ ∫ B 2 e - x 2 + y 2 d x d y
Determine o volume dos sólidos W abaixo. W é limitado pelas superfícies z = x 2 + y 2 , x 2 + y 2 = 4 , x 2 + y 2 = 9 e o plano z = 10 .
Calcule int int_D (e^(((x + y)/(x - y))))/((x - y)^2) d x d y , ondeD = {(x , y) in R^2,1 = (x - y)^2 = 4 , y = 0 e x + y = 0}