Seja
- Transforme em uma só integral iterada na ordem invertida.
- Calcule para
Passo 1
A região que ele descreve ali é do tipo I, e está separada em dois intervalor
Vamos fazer o gráfico dessas partes.
O primeiro pedaço é uma reta, mas e o segundo pedaço? Vamos dar uma arrumada algébrica nele p ver que, na verdade, é uma circunferência.
Aqui vamos completar quadrado
Temos a nossa circunferência, o gráfico dessa bagunça vai ser
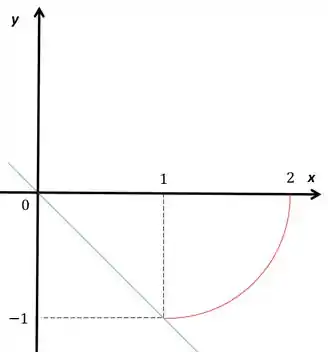
Só desenhei as parte que importam da circunferência, para escrevermos como uma região do tipo , precisamos achar os limites de e as funções que varia. Conseguimos perceber o intervalo de
Passo 2
Vamos ver agora com calma o intervalo de
Ele vai da reta até a circunferência, vamos ver como é a parte da circunferência
Eu peguei a parte positiva da raiz por que estamos pegando o lado direito da circunferência, direito em relação ao centro ok?
Então
E além disso ele é maior que a reta
Vamos ter
Passo 3
A integral vai ficar
Passo 4
Como tanto a função que vamos integrar como a região de integração possuem termos e , vamos utilizar coordenadas polares. Faremos, então:
Passo 5
Agora que já definimos a substituição que faremos, vamos analisar os novos intervalos de integração.
Repara que o ângulo vai variar de um extremo da circunferência até o outro. Olha o desenho com o ângulo marcado
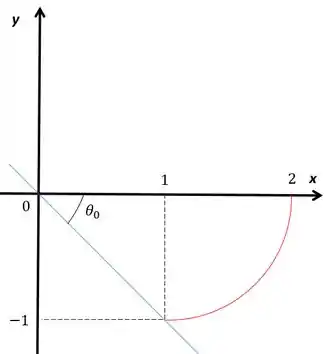
Vamos ter
E
Isso porque ele vai até o eixo que é onde começamos a contar a parada.
O raio da curva vai variar de até a curva vermelha, vamos ver isso algebricamente,
Agora o limite superior, que é o da circunferência.
Como
Vamos ter
Passo 6
Vamos montar a integral com coordenadas polares
Passo 7
Temos que achar a integral
Para isso vamos fazer
Vamos fazer
A integral vai ficar
Desubstituindo o valor de
Passo 8
Vamos ter