UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 5.1c
Determine a equação da reta tangente ao gráfico das seguintes funções, no ponto de abscissa
dada:
Passo 1
Eaew, belezinha?
O enunciado pede para obtermos a equação da reta tangente ao gráfico da função y(x) no ponto que possui coordenada x = 0. A gente sabe que uma reta é uma função bastante simples, porque só tem dois parâmetros que definem uma reta: seu coeficiente angular e seu coeficiente linear. Então, se a gente conhece dois pontos contidos em uma reta ou então um dos coeficientes e um ponto, já temos informação suficiente para obter toda a equação! Bem, primeiro, a gente sabe que o ponto do gráfico y(x) que possui coordenada x = 0 é o ponto (0,1), porque . Então, a gente sabe que, qualquer que seja a equação da nossa reta tangente ao gráfico no ponto de abscissa x =0, ela deve passar pelo ponto (x,y) = (0, 1), beleza? Excelente! Agora só precisamos determinar um coeficiente da reta! E como é que a gente pode fazer isso? Podemos calcular a derivada de y(x) para obter o coeficiente angular! Quer saber como faz isso? Dá uma olhada!
Passo 2
Bem, a gente sabe que a derivada de uma função y(x) nos dá uma outra função y’(x) que, para cada ponto x, nos retorna a inclinação da reta tangente à curva no ponto em questão. Então vamos derivar a função y(x)? Então… sabemos que a derivada da função é ela mesma. Mas tem um porém… A função que queremos derivar não é exatamente , ela é , não é? E agora? Bem, não tem problema! A gente pode usar a regra da cadeia para derivar y(x) se reconhecermos que como uma função composta! Se definirmos e , vemos que y(x) nada mais é do que a função composta . Então, para derivarmos essa função fazemos
Perfeito! Agora temos uma função que vai nos dar o coeficiente angular da reta tangente para qualquer x. Como a gente quer saber o coeficiente angular para o ponto com abscissa x = 0, só precisamos substituir x=0 na função y’(x). Fazendo isso, a gente obtém
Passo 3
Tá, mas e daí? E agora, como a gente monta a equação da reta tangente? Ora, veja bem: a gente sabe que a equação da reta tem o formato
Bem, a gente já tem o valor de a, mas… como que a gente acha b? Aí que entra a informação do ponto que calculamos que pertence tanto à reta tangente quanto à função y: (0,1). O que esse ponto nos diz? Ele diz que, quando x = 0, o valor do f(x) da reta é 1. Assim a gente consegue determinar o valor de b, fazendo
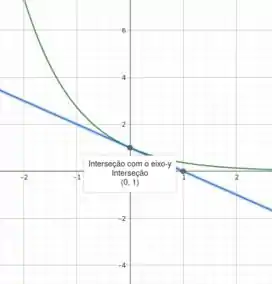
Então, o nosso b vale 1. Agora, a gente já tem o valor do coeficiente angular e do coeficiente linear e a equação da reta está completamente determinada! Vamos dar uma olhada no gráfico dessa situação: a gente tem uma reta em azul que corta o eixo y no valor b = 1 e que passa pelo ponto (0, 1) tangente ao gráfico da função em verde .
