Exercícios Resolvidos de Reta tangente

Ver Teoria

Exercício 222 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

Enunciado

UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 2ª Lista de Exercícios, Questão 5.5

Encontre a reta tangente à astroide + , em que a > 0 é um constante, em um

ponto da curva.

Passo 1

Eaew, belezinha?

O enunciado nos pede para calcular a reta tangente à astroide em um ponto arbitrário . Bem, a gente sabe que para calcular a inclinação de uma função precisamos calcular a sua derivada. No entanto, precisamos notar que mesmo se escrevermos y em função de x, uma astroide não é uma função, porque para cada x existe mais de uma imagem, visto que tanto valores positivos da raiz quanto negativos são solução para y(x). Mas, nem tudo está perdido! Apesar de não podermos escrever a astroide inteira como uma função, sabemos que ela é simétrica em x. Dá uma olhada na figura abaixo:

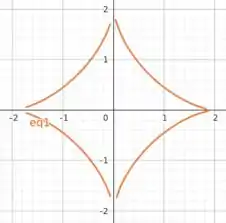
Da figura, devido a simetria da astroide, a gente percebe que, para um dado x, teremos uma inclinação da reta tangente para a parte positiva da função (correspondente à ) e uma inclinação da reta tangente para a parte negativa (correspondente à ) que serão iguais em módulo para o mesmo x, visto que a única distinção entre as curvas é o sinal. Então, vamos nos restringir a determinação da inclinação da reta tangente para a parte positiva. Então, bora lá!

Passo 2

Bem, agora nossa missão é derivar em relação a x. Para isso, vamos utilizar a regra da cadeia. Definindo as funções e , podemos escrever a função y(x) como . Pela regra da cadeia, temos que a derivada de y em relação à x é:

Logo, a inclinação da reta tangente a um ponto de coordenadas é . Esse é o nosso coeficiente angular. Agora precisamos determinar o coeficiente linear da reta . Para um ponto sobre a astroide de coordenadas , temos que o coeficiente linear é dado por . Então, substituindo a expressão encontrada para o coeficiente angular, obtemos:

Assim, a equação da reta tangente à um ponto da astroide é dada por

Para a parte negativa da astroide, tudo que precisamos fazer é trocar o sinal da “função” , o que nos renderá o mesmo coeficiente angular no ponto , mas com sinal trocado.