UFJF, Sem Campus, Cálculo 1, AV3 - 2019.1, Questão 8
Uma particula se desloca sobre o gráfico da fun ̧c ̃ao
no quadrante de forma que sua coordenada é o vértice de um triângulo retângulo como na figura abaixo.
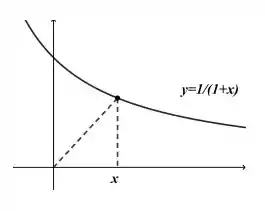
Se a taxa de variação da coordenada é constante igual a , determine a taxa de variação área do triângulo no instante em que .
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de cálculo 1. Dessa vez uma envolvendo taxa relacionada
Nosso objetivo é determinar a taxa de variação da área do triângulo no instante em que .
? Onde o nosso triângulo é formado segundo a figura a seguir
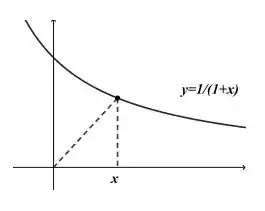
Para podermos resolver essa questão precisamos entender melhor o que está acontecendo.
O eixo do nosso triângulo se move conforme a figura acima, o enunciado diz que está se movendo a uma velocidade constante de .
Ou seja, o enunciado já nos diz que é a variação do eixo , isto é:
Mas queremos saber a taxa de variação da área do triângulo. Então se representa a áre, queremos saber
Quando . Bem, vamos trabalhar com isso.
Passo 2
Agora, vamos usar a fórmula da área do triângulo para conseguir alguma relação entre a área e . Usando a imagem acima, vemos que a área é:
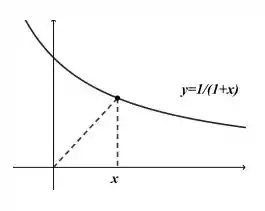
Agora, podemos usar derivadas implícitas para obtermos
Passo 3
Derivando implicitamente
(estamos enfatizando que são funções de )
Temos:
Calculando a derivada de em relação a , temos:
Usando a regra da derivada da divisão
Ou seja descobrimos que
Agora, podemos substituir isso na expressão
Olhá só, apareceu o nosso termo de interesse . Agora só precisamos substituir os valores que calculamos anteriormente. Queremos quando . E por último, vimos no passo 1 que o enunciado diz que . Substituindo esses valores na equação acima temos:
substituindo os valores
Ou seja, a taxa de variação da área do triângulo quando é
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊