Seja
- Calcule a derivada de
- Determine a equação da reta tangente ao gráfico de em
- Determine os intervalos de crescimento e decrescimento de para
Passo 1
Letra a) CUIDADO! Embora pareça um problema de integração, aqui você não precisa calcular nenhuma integral não!
Ué, mas como você sabe disso?
Sei, porque ele pediu a derivada, e tem como da gente derivar uma integral dessa forma sem calcula-la, bastando aplicar o teorema fundamental do cálculo!
Me acompanha aqui ;D
Passo 2
O teorema fundamental do cálculo nos diz o seguinte:
Onde por comparação com os dados que a gente têm
Podemos dizer que
Perceba em primeira mão que , portanto aquele primeiro termo do teorema desaparece, no nosso caso
, portanto
Agora, quem é esse termo aqui ?
Pow, esse termo aí tá nos dizendo para no lugar de , jogar a função , ou seja
Portanto
Passo 3
Letra b) Pow, primeiramente quem é o ponto ? A coordenada ta ok, mas e essa ?
Temos que descobrir isso antes de qualquer coisa
Mas cara, se ele te deu a função , joga o lá e vamos ver no que vai dar, bora?
Então vem comigo calcular essa integral aí.
Passo 4
Pra gente resolver essa integral, devemos antes passar aquele termo para dentro da raiz, o que não é muito complicado, pois basta elevar ele ao quadrado de volta, dessa forma aqui
Como temos uma raiz aí, podemos pensar em fazer uma substituição de forma que cancele essa raiz, ou seja, vamos chamar de
Porque assim , percebeu?
Toda mudança nos pede que troque os limites de variação...
substituindo tudo...
Passo 5
Podemos agora, para resolver essa integral aí, fazer uma integração por partes, onde o vai ser o que vai derivar, pois assim ele desaparece, percebeu?
Logo, comparando com a fórmula de integração por partes...
comparando
essa outra integral mata direto ;D
Logo
substituindo os limites
Logo, concluímos que o ponto que queremos é .
Passo 6
Cara, a gente sabe lá da definição de derivada que ela é a o coeficiente angular da reta tangente, então a reta tangente se escreve
onde o é a derivada no ponto que a gente quer calcular, ou seja, já vimos que
então
então, a reta tangente é
Pra encontrar , basta substituir o ponto , que está em cima da reta tangente, ou seja
Logo, a reta tangente é
Passo 7
Letra c) então, para determinar os intervalos de crescimento e decrescimento da função, a gente tem que analisar aqui o sinal da primeira derivada, lembra?
Mas calma que a gente só quer avaliar isso, dentro do intervalo , heim!
Pow! a gente já viu que , mas como a gente vai analisar em um intervalo positivo, não necessitamos desse módulo, pegou?
Vamos fazer o seguinte agora:
- Primeiro vamos fazer um esboço do gráfico do cosseno
- Depois vamos fazer o mesmo para a função
- analisar o produto de cada uma separadamente e depois fazer o produto deles, sacou?
Passo 8
Vamos começar com o gráfico do cosseno.
Já temos uma noção desse gráfico, basta agora a gente determinar os pontos que ele toca o eixo dentro desse limite dado.
O cosseno só é , quando
nesses casos, podemos determinar dentro do intervalo de que isso acontece, que no caso é
O próximo seria que já está fora do intervalo, percebeu?
Desenhando esse cosseno
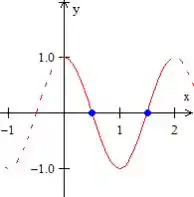
Passo 9
Vamos analisar agora o sinal da função .
Bem, essa daí é uma reta que passa pela origem e decrescente, ou seja
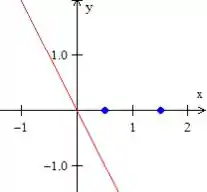
ela é negativa no nosso intervalo
Passo 10
Multiplicando os sinais de uma com a outra, ou seja
De 0 até ½
De ½ até 3/2
De 3/2 até 2
Negativo
Negativo
Negativo
Positivo
Negativo
Positivo
(produto das duas)
Negativo
Positivo
Negativo
Portanto, onde o sinal da deriva é positivo, ou seja de até , podemos dizer que a função cresse, já nos outros dois, ela decresce
Resposta
Letra a)
Letra b)
Letra c)