Seja . Admita que .
Determinar os intervalos abertos nos quais é estritamente crescente e nos quais é estritamente decrescente;
Passo 1
Em primeiro lugar, olhamos para para determinar o domínio. O força o domínio a ser . Agora, para decidir se decresce ou cresce devemos olhar para a derivada: onde é positiva cresce, onde é negativa decresce. Já recebemos a derivada:
Temos que é negativo em e positivo de até , assim terá os sinais exatamente trocados em relação ao . Já o tem seu sinal dependente de apenas, como o domínio começa a partir de , é sempre positivo.
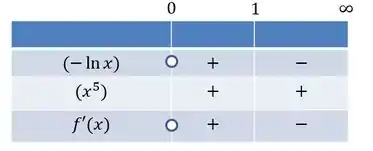
Concluímos, então, que é crescente entre e e decrescente a partir daí, com o detalhe de que temos um ponto crítico de máximo no .