- Considere a função cujo gráfico está representado abaixo. Determine os pontos de continuidade e descontinuidade de
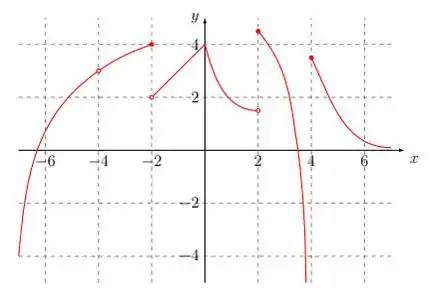
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos que dizer quando a função é contínua e nós podemos fazer isso de duas maneiras: olhando seu gráfico ou usando a definição.
Aqui como nós temos o gráfico, vamos fazer visualmente. É simples, sabe quando você pega pra desenhar alguma coisa, aí você vai passando o lápis na folha e não tira? É exatamente isso, uma função é contínua não tem interrupções.
Então vamos escrever quais intervalos do gráfico nós conseguimos desenhar sem tirar o lápis do papel!
Passo 2
Olhando para o gráfico, podemos destacar as regiões sem interrupção de azul:
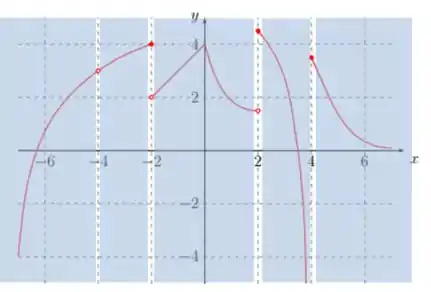
Repara que a função é descontinua em
E ela é continua em
Prontinho!
Resposta
No texto.