UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Prof° Ricardo Martins - Listas sobre Limites e Continuidade, Questão 1.12
Mostre que a função
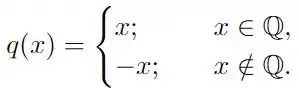
é contínua na origem.
Passo 1
Oiie, tudo certinho?
Temos aqui a seguinte função
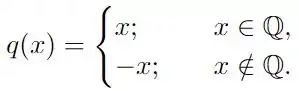
definida de formas diferentes se estivermos com números dentro dos racionais, ou números que não pertencem aos racionais. Mas, quem são os racionais? Os racionais contém os números naturais, inteiros, frações e dízimas periódicas! Bastante coisa certo? Ou seja, eles contém a origem . Mas, quem não pertence aos racionais? São números como por exemplo , que são decimais, mas não periódicos! Sabendo isso, vamos tentar verificar a continuidade da função na origem, através de
e, precisamos também que
em que é um valor dentro do domínio da função! Vamos tentar verificar isso! Saca só!
Passo 2
Como temos que analisar os limites na origem, ou seja
precisamos nos preocupar apenas com valores que estão próximos de . Isso é o suficiente para garantir a nossa continuidade. Note que todo número que pode ser escrito como uma fração é racional, ou seja, todos os números a seguir
e, assim por diante, são todos racionais!Pois podem ser escritos como frações da forma
mas como isso nos ajuda? Vamos lembrar a definição formal de limite! Saca só!
Passo 3
A definição formal (ou precisa) de limite diz que
tal que se então
em nosso caso temos que e se e se . Da desigualdade envolvendo , podemos escrever que
ou, como é uma função modular, podemos dizer que
e, a outra desigualdade é da forma
ou seja, temos que
Note então que obter , significa escolher e próximos a . Como esse número pode ser arbitrariamente pequeno, sempre iremos podemos analisar as proximidades do limite em usando valores da forma
não importa se temos um número irracional nas proximidades da origem, sempre podemos escrever um número irracional menor, ou irrelevantemente diferente, no contexto do limite. Sendo assim, temos que a função nas proximidade de pode ser tomada sempre como um racional, e portanto, os limites laterais são
e, a função é simplesmente
ou seja, a função é contínua! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!