Questão 2:
Seja o campo
- Justifique se é conservativo ou não sem calcular potenciais.
- Caso ser conservativo, calcule os potenciais para .
- Seja o campo
Calcule onde é o segmento de até .
Passo 1
Pow, pela teoria sabemos que se o rotacional de um campo for e esse campo estiver definido em toda região que estamos trabalhando, ou seja, se ele não tiver singularidades, ele é conservativo.
Vamos averiguar primeiro o rotacional...
Onde
Calculando a primeira derivada parcial
Atenção na regra da fração...
Calculando a segunda
Olha a regra da fração novamente...
Voltando para o rotacional...
Rotacional nulo e com o campo sem singularidades...
Para , o campo torna-se conservativo. :D
Passo 2
Pois então, para calcular as funções potenciais, vamos usar uma preciosa informação, a teoria: se é uma função potencial de então . WHAT???
Calma! Esse aí é a função potencial, o que a gente vai fazer igualar o seu gradiente ao campo dado!
Portanto
Passo 3
Pegando a segunda, já que está mais fácil...
E integrando com relação a , vamos obter
Note que apareceu uma função que depende de apenas, pois se derivando em relação a ela desaparece, integrando em relação a ela aparece. Sacou? :)
calculando essa integral aí com relação a (tomando como uma constante), teremos
Essa outra integral, sai com uma substituição...
Voltando para a variável...
Passo 4
Note que já ganhamos a função potencial, porém temos ainda que ver quem essa função de é. Para fazer isso, vamos derivar com relação à agora e igualar com a função acima.
Derivando então essa com relação à ..
Calculando essa segunda derivada aplicando a regra da cadeia...
Essa última derivada, como é uma função que depende só de , essa derivada vira uma derivada simples...
Igualando à
Cortando esses caras e simplificando, teremos
Integrando agora com relação a ...
Note que é a constante de integração, mas que poderemos considerar , já que o problema nos pediu apenas uma função potêncial...
Passo 5
Voltando para o problema inicial... Uma função potencial de é
Passo 6
O problema agora nos pede para calcular a integral de linha...
Onde o é o campo...
Note que podemos separar esse campo aí em uma soma de dois outros...
Ou seja, se chamarmos ...
O bom de fazer isso é que já calculamos uma função potencial para e isso vai facilitar. Veja...
Passo 7
Como queremos uma integral de linha para em cima do segmento ...
Para a integral de linha em cima de se calcula muito fácil, afinal de contas, temos a função potencial dele, informações do ponto de saída
e do ponto de chegada
Então...
Então...
Enquanto que...
Logo...
Passo 8
Bem, mas ainda nos falta encontrar
E aqui não tem jeito. Temos que calcular essa integral de linha direta:
1º - Parametrizando a curva .
2º - Encontrando o termo .
3º - Substituindo a parametrização no campo .
Passo 9
Para parametrizar a curva , vamos desenha-la... Sabemos que ela é um segmento de reta que une o ponto e ...
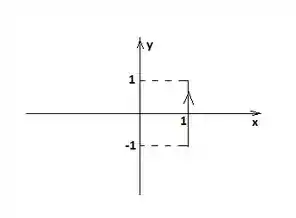
Epa! É um segmento paralelo ao eixo passando por ...
Então...
Como é e varia de a , então...
Passo 10
Encontrando o termo ...
E substituindo os termos da parametrização no campo...
Voltando para a integral de linha...
Agora é só calcular essa integral aí ;)
Passo 11
Voltando então para a integral de linha principal que queríamos calcular...
E substituindo...
Resposta
O campo é conservativo.