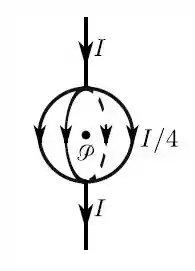
Uma corrente estacionária, de intensidade , flui ao longo de um segmento retilíneo que se divide, igualmente, em quatro meridianos de uma esfera de raio , perpendiculares (dois a dois) entre si, e reencontrando-se num outro segmento retilíneo. Qual é o módulo do campo magnético no centro da esfera?
Passo 1
É a Lei de Biot-Savart que nos dá a fórmula para calcular campo magnético produzido por uma corrente né?
É ela que vamos usar!!
Mas pera, vamos analisar primeiro os segmentos retilíneos e depois os segmentos semicirculares, beleza?
Passo 2
Então bora analisar os segmentos retilíneos.
Para os dois segmentos retilíneos os vetores e , para o cálculo do campo no ponto P, estão alinhados, ou seja, o ângulo entre eles é ou . Para esses casos podemos mostrar que:
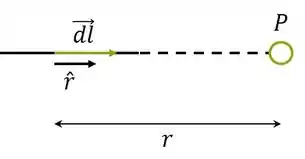
Então, os segmentos retilíneos não contribuem para o campo no ponto P.
Passo 3
Agora, nos resta analisar os segmentos semicirculares. Para achar o campo produzido por cada um desses segmentos no ponto P precisamos calcular essas quatro integrais.
SÉRIO?? :/
Calma! O truque neste caso é se aproveitar da simetria.
Vamos analisar primeiro o campo produzido por um par de segmentos semicirculares que estão um frente ao outro. Podemos aplicar a lei de Biot-Savart sobre todo o comprimento dos dois segmentos e teremos esse resultado:
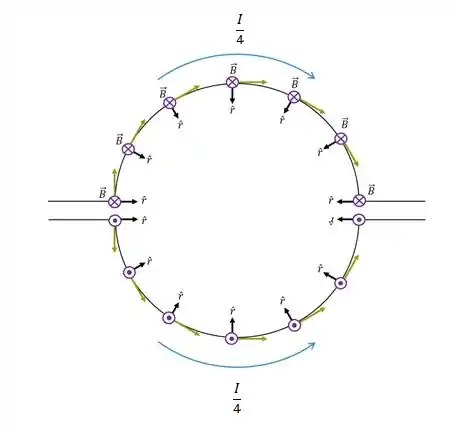
Pela figura podemos perceber que os campos produzidos por cada segmento possuem a mesma direção, mas sentidos opostos.
Note também que a corrente que passa pelos dois segmentos é a mesma, o comprimento dos dois segmentos é o mesmo e a distância dos segmentos para o ponto P também é a mesma, pois o ponto P é o centro da semicircunferência. Então nós temos que o módulo dos campos produzidos é o mesmo.
Então os campos se anulam e o campo resultante desse par será zero no ponto P.
Analogamente, o outro par vai zerar também.
Logo, o campo total é:
Resposta
Letra c