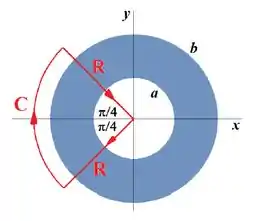
Um fio reto, infinito e oco (de raio interno e externo ) centrado no eixo tem a seção transversal (no plano mostrada na Figura. Este fio é percorrido por corrente com densidadeno sentido , onde . Determine:

1. A corrente total em seção transversal arbitrária do fio.
2. O vetor do campo magnético em um ponto arbitrário cuja distância ao eixo é
3. O vetor do campo magnético em um ponto arbitrário cuja distância ao eixo é
4. O vetor do campo magnético em um ponto arbitrário cuja distância ao eixo é
5. O valor de ao longo do contorno orientado mostrado na figura, formado por duas radiais de comprimento e um quadrante de círculo de mesmo raio.

Letra (b):

Para não temos corrente envolvida, então o campo magnético é nulo nessa região:

Letra (c):

Pela lei de Ampére o campo em um fio tangencia o círculo de raio e tem a seguinte expressão:

Então para temos:

Aqui usei a expressão que a gente achou no item (a) e substituí por =), beleza?

Letra (d):

E agora para vou usar a mesma expressão do item (a) para a corrente, já que temos toda corrente envolvida nessa região e o campo magnético é:

Letra (e):

Vamos calcular a da lei de Ampére, mas antes, vamos pensar um pouquinho. Queremos um quadrante certo? Então a parte da corrente que queremos é da corrente total encontrada no item (a), assim o valor de fica:

Beleza?

Pronto pra próxima questão? =)