O fio condutor fino mostrado na figura abaixo é formado por dois trechos retilíneos e
semi-infinitos, paralelos ao eixo de um sistema de coordenadas, unidos por um trecho semicircular de raio contido no plano e centrado na origem. Este fio transporta uma corrente estacionária de intensidade , no sentido indicado na figura. Nessa situação, determine, justificando cuidadosamente todo o desenvolvimento:
(a) O vetor campo magnético resultante produzido pelos dois trechos retilíneos na origem.
(b) O vetor campo magnético produzido pelo trecho semicircular na origem.
(c) O vetor campo magnético resultante produzido pelo fio na origem e o módulo deste campo.
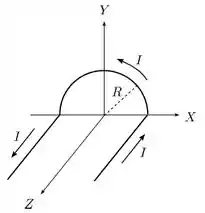
Passo 1
a)O campo magnético vai ser dado pela lei de Biot-Savart
Vamos começar calculando o campo magnético para a linha à esquerda do eixo (na figura). Nesse caso, está posicionado no ponto e é dado por
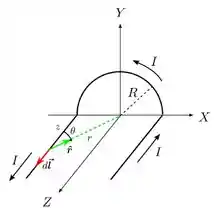
Pela figura acima, sabemos que
Onde .
Substituindo na lei de Biot-Savart:
Mas esse é um campo magnético para um elemento infinitesimal, para encontrarmos o campo total produzido, vamos integrar de a
Para o fio localizado à direita do eixo , o procedimento é exatamente igual, obtendo o mesmo resultado para , então:
Passo 2
b)Mais uma vez, vamos utilizar a lei de Biot-Savart ta bom? Mas dessa vez, é tangente à semicircunferência e em todos os pontos da semicircunferência. Então temos que
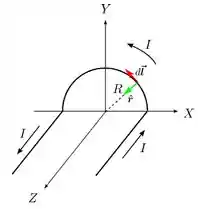
Pela lei de Biot-Savart:
Integrando, temos que
Então, o campo magnético no semicírculo é dado por:
Passo 3
c)O campo magnético total será dado pela soma do campo magnético nas linhas com o campo no semicírculo:
O módulo desse campo será dado por